Предположим, что у нас есть функция (график этой функции – это парабола) и необходимо построить график функции . Вычислим значения некоторых точек для графиков этих функций.
Из таблиц видно, что одним и тем же значениям аргумента соответствуют противоположные значения функций. Графически это означает, что графики расположены симметрично относительно оси абсцисс. То есть заданная парабола () зеркально отобразится относительно оси (см. Рис. 1).
Рис. 1. Графики функций и
Таким образом, если у нас есть произвольный график , то для построения графика необходимо график симметрично отразить относительно оси (см. Рис. 2). Такое преобразование называется преобразованием симметрии относительно оси .
Рис. 2. Преобразование симметрии относительно оси
Преобразование симметрии – зеркальное отражение относительно прямой. График получается из графика функции преобразованием симметрии относительно оси .
На рисунке 3 показаны примеры симметрии относительно оси .
Рис. 3. Симметрия относительно оси Ox
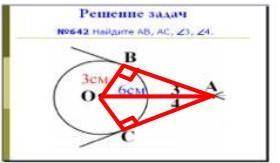
угол 3=30
угол 4= 30
угол ВАС=60
угол ВОС=120
Пошаговое объяснение:
Треугольник ОВА прямоугольный, тк угол между радиусом и касательной равен 90 градусов. В прямоугольном треугольнике катет равен половине гипотенузы, если он лежит против угла в 30 градусов, следовательно угол 3 равен 30 градусов. Найдем угол ВОА, зная, что сумма углов треугольника равна 180 градусов. Угол ВОА=180-(Угол ОВА+Угол 3)=180-(90+30)=180-120=60
Треугольники ОВА и ОСА равны по катету (ОВ=ОС тк это радиусы одной окружности) и гипотенузе (ОА общая), следовательно угол 3 равен углу 4 и равен 30 градусам, а угол ВОА равен углу СОА и равен 60 градусам. Тогда угол ВАС равен угол 3+угол4=30+30=60, а угол ВОС=уголВОА+уголСОА=60+60=120 градусов