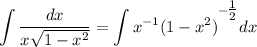
Для вычисления интеграла от дифференциального бинома
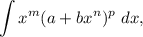
где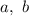 
— действительные числа, a 
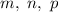— рациональные числа, также применяется метод подстановки в следующих трёх случаях:
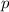— целое число, то используется подстановка 
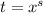, где 
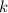— общий знаменатель дробей 
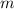и 
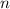;если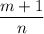 
, то используется подстановка 
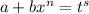, где 
— знаменатель дроби 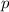;если 
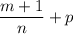, то используется подстановка 
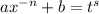, где — знаменатель дроби 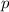;Для данного интеграла проверим второй случай: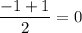 
, следовательно, сделаем замену: 
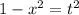. Тогда 
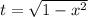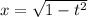и 
и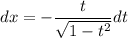 
, если ![x \in [-1; \ 1]](/tpl/images/1066/7338/3c7ad.png)
. Имеем:
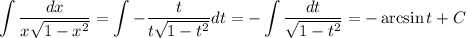
Сделаем обратную замену:
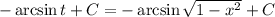
ответ: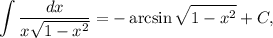 
если ![x \in [-1; \ 1].](/tpl/images/1066/7338/49302.png)
67 цифр.
Пошаговое объяснение:
Чтобы решить данную задачу,нужно вспомнить что такое цифры и числа.
Цифры - это десять знаков: 0,1,2,3,4,5,6,7,8,9.
С цифр мы записываем числа.
Числа (натуральные) - это те числа,которые используют при счёте предметов. Натуральный ряд бесконечен,наибольшего числа нет.
Нам нужно узнать, сколько цифр мистер Фокс записал на доске. Приступим к решению задачи:
1) a-b+1,41-7+1=35 - чисел записали на доске.
2) 7,8,9-одназначные числа.
35-3=32-двузначных чисел.
3) 32×2=64 - цифр в двузначных числах.
4) 64+3=67 - цифр мистер Фокс записал на доске.
3,2а-0,7а=11,77
2,5а=11,77
а=11,77/2,5 | умножаем на 100 ( если вам нужна дробь)
а= 1177/250
а=4,708
ответ :4,708
2)15,05b+3,2b-b=34,5
17,25b=34,5
b=34,5:17,25
b=2
ответ : 2