ответ: 5 и 17.
Обозначим искомые числа за x и y. Тогда: x + y = 22.
Если сумма двух чисел - это четное число, то оба числа были одной и той же четности (то есть либо оба нечетные, либо оба четные).
Но и разность чисел одной четности - это тоже четное число. Поэтому x - y - это обязательно четное число. Но среди чисел меньше 14 и больше 10 только одно четное число, это 12 (считаем, что разность не может быть равна 10 и 14).
Тогда мы можем составить и решить эту систему уравнений:
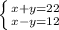
Сложим эти уравнения:
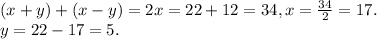
Получается, Сережа загдал числа 5 и 17.
Примечание.
Если же все-таки сумма может быть равна 10 и 14, то роме этой пары еще подойдут пары (19, 5) и (17 и 7).
Искомое число должно делиться на 4•3, т.е. на каждый делитель числа 12.
Число делится на 3, если сумма всех его цифр делится на 3.
На 4 делятся только те числа, которые заканчиваются на два нуля или на две цифры, выражающие число, которое делится на 4.
Поэтому в искомом числе
7*462* - последняя цифра может быть только 0, 4, 8
а) Пусть последняя цифра будет 0.
Тогда сумма 7+4+6+2=19. До числа 21, которое делится на 3, не хватает 2. Ставим 2 вместо первой звездочки, получим
724620, и это число нацело делится на 12.
До числа 27, которое делится на 3, не хватает 8.
784620- делится нацело на 12.
б) Подставив в конец числа цифру 4, таким же образом находим, что вторая тоже 4.
744624
Если последняя цифра 8, то вторая должна быть 0.
704628
Наибольшим из найденных чисел является 784620, наименьшим 704628