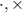 . Второй используется в случае переноса на новую строку или для наглядности. Например,
. Второй используется в случае переноса на новую строку или для наглядности. Например, 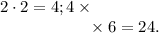
 , но в начальной школе про это можно не знать. Числа, соединённые знаком умножения, называют множителями, а результат операции - произведением.
, но в начальной школе про это можно не знать. Числа, соединённые знаком умножения, называют множителями, а результат операции - произведением. , либо записывают в виде дроби:
, либо записывают в виде дроби: 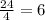 .
.
2) (2x+у)³ = 8x³ + 12x²y + 6xy² + y³
3) (2a-3)³ = 8a³ - 36a² + 54a - 27
1) (a+b)² - (a-b)² = 4ab
a² + 2ab + b² -a² + 2ab - b² = 4ab
4ab = 4ab
2) а²+b²=(а+b) ²-2аb
а²+b²=а²+2ab +b² - 2ab
а²+b²= а²+b²
3) а²+b²=(а-b) ² + 2аb
а²+b²=а²- 2ab +b² + 2ab
а²+b²= а²+b²