ответ: шерстяных тканей 115м; шелковых тканей 165м
Пошаговое объяснение:
Узнаем сколько всего тканей в магазине: для этого количество хлопчатобумажных тканей разделим на 2/9:
80/(2/9)=80*9=2=360м
Узнаем сколько шелковых и шерстяных тканей в магазине: для этого из общего количества тканей вычтем количество хлопчатобумажных тканей: 360-80=280м
Примем количество шерстяных тканей за х, а количество шелковых тканей х+50.
Составим уравнение: х+(х+50)=280
2х=280-50
2х=230
х=115м - это количество шерстяных тканей
количество шелковых тканей равно: 115+50=165м
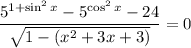
1. Уравнение вида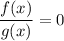 
равносильно системе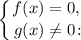 
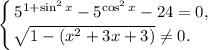
2. Решим уравнение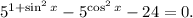 
2.1. Поскольку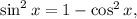 
то
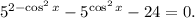
2.2. Используя свойство степеней 
имеем:
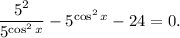
2.3. Сделаем замену: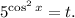 
Тогда:
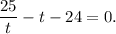
2.4. Преобразуем уравнение:
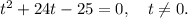
2.5. По теореме, обратной теореме Виета, имеем:
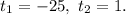
2.6. Делаем обратную замену:
2.7. Первое уравнение не имеет корней, поскольку правая часть не может быть отрицательной. Решим уравнение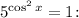 
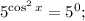
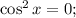
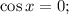
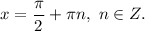
3. Определим ограничения: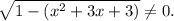 
3.1. Ограничение для данного уравнения соответствует неравенству:
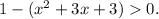
3.2. Раскроем скобки, приведем подобные слагаемые:
3.3. Умножим обе части неравенства на 
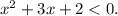
3.4. Решением данного неравенства является промежуток 
4. Отберем корни уравнения, принадлежащие промежутку
Пусть 
тогда 
Пусть 
тогда 
Пусть 
тогда 
5. Решением данного уравнения является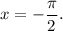 
6. В ответ следует записать сумму корней (или корень, если он единственный), деленную на 
ответ: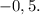 
|х+3|=9-4,
|х+3|=5,
х+3=5, х+3=-5,
х=2. х=-8.
ответ: -8; 2.
2) |y-2|+8=5,
|у-2|=5-8
|у-2|=-3
ответ: нет корней.
3) 1,7|х|+4,9=10,
1,7|х|=10-4,9,
1,7|х|=5,1,
1,7х=5,1, 1,7(-х)=5,1,
х=3. х=-3.
ответ: -3; 3.
4) 2,5|3y|=15,
2,5·3у=15, 2,5·(-3)у=15,
у=2. у=-2.
ответ: -2; 2.