1. в ящике 120 кг пшена. после того как из ящика отсыпали пшено в мешок, в ящике осталось 65% всего пшена. сколько кг пшена вошло в мешок?
решение: 120*0,65=78кг осталось в мешке
120-78=42 кг пшена вошло в мешок
ответ: 42 кг
2. в роще 700 берёз и 300 сосен. сколько поцентов всех деревьев составляют сосны?
решение: всего в роще 1000 деревьев
(300/1000)*100=30 % всех деревьев
ответ: 30 %
3. СО СКЛАДА ВЫГРУЗИЛИ 244,8 Т УГЛЯ, ПОСЛЕ ЧЕГО НА СКЛАДЕ ОСТАЛОСЬ 55% УГЛЯ. СКОЛКО ТОНН УГЛЯ БЫЛО НА СКЛАДЕ?
решение: 244,8 т = 45%
х = 100 %
х=(244,8*100)/45 = 544 т
ответ: 544 т
4. Товар стоил 4800 рублей.Перед праздниками его цена снизилась на 12%.Какова новая цена товара?
решение: 4800*0,88=4224 рублей
ответ: 4224 рублей
5.Решите уровнение: 1,7Х+21+3,1Х=57
решение: 4,8х=36
х=7,5
ответ: 7,5
6. В пакете лежали сливы. Сначала из него взяли 50% слив,а потом 40% остатка. После этого в пакете осталось 3 сливы.Сколько слив было в пакете первоночально?
решение: 1. 3 - 60%
х - 100%
х= 5 слив
2. 5 - 50%
х - 100%
х = 10 слив
ответ: 10 слив
ДАНО
Y = x³ - 3*x² + 4
1.Область определения D(x) - Х∈(-∞;+∞) - непрерывная.
Вертикальных асимптот - нет.
2. Пересечение с осью Х. Y= (x-2)²(x+1). Корни: х₁,₂ = 2, х₃ = -1.
3. Пересечение с осью У. У(0) = 4.
4. Поведение на бесконечности.limY(-∞) = - ∞ limY(+∞) = +∞.
Горизонтальной асимптоты - нет.
5. Исследование на чётность.Y(-x) ≠ Y(x).
Функция ни чётная ни нечётная.
6. Производная функции.Y'(x)= 3*x² - 6*х = 3*х*(х - 2) 0 .
Корни: х₁=0 , х₂ = 2.
Схема знаков производной.
_ (-∞)__(>0)__(x1=0)___(<0)___(x2=2)__(<0)_____(+∞)__
7. Локальные экстремумы.
Максимум Ymax(-1)= 4, минимум – Ymin(2)=0.
8. Интервалы монотонности.
Возрастает - Х∈(-∞;0)∪(2;+∞) , убывает = Х∈(0;2).
8. Вторая производная - Y"(x) = 6*(x - 1)=0.
Корень производной - точка перегиба Y"(1)= 0.
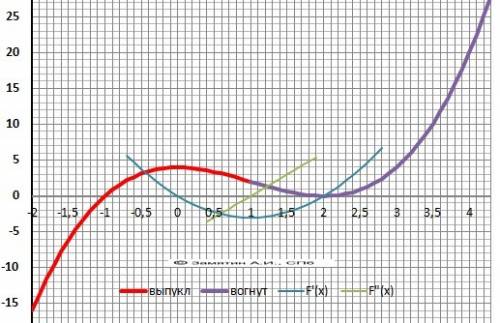
9. Выпуклая “горка» Х∈(-∞;1), Вогнутая – «ложка» Х∈(1;+∞).
10. Область значений Е(у) У∈(-∞;+∞)
11. Наклонная асимптота. Уравнение: lim(oo)(k*x+b – f(x).
k=lim(oo)Y(x)/x. b = lim(oo)Y(x) – k*x. Наклонной асимптоты - нет
12. График в приложении.