Пошаговое объяснение:
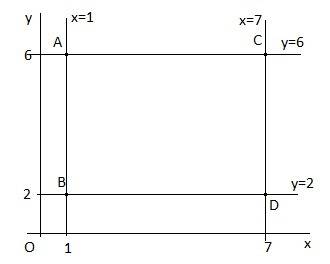
Отметим точки A, B и C на координатной плоскости. У точек A и B совпадают абсциссы точек, соединяем их прямой x = 1.
У точек A и C совпадают ординаты точек, соединяем их прямой y = 6.
Через точку B с ординатой 2 проводим прямую y = 2 параллельную прямой y = 6 (противоположной стороне прямоугольника).
Через точку C с абсциссой 7 проводим прямую x = 7 параллельную прямой x = 1 (противоположной стороне прямоугольника).
Проведенные через точки B и C прямые пересекутся в точке D(7; 2), которая и будет 4 вершиной прямоугольника ABCD.
(х+8) - длина прямоугольника
х*(х+8)=209
решим квадратное уравнение:
x²+8x-209=0
D=b²-4ac=64-4*1*(-209)=900
x1,2=(-b±sqrtD)/2a=(-8±30)/2
x=22/2=11 (отрицательный корень отбрасываем, длины не могут быть отрицательными)
ширина равна 11 см, длина равна 11+8=19 см
периметр равен Р=11*2+19*2= 22+38=60 см