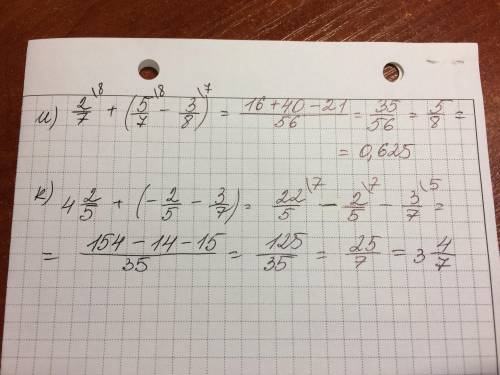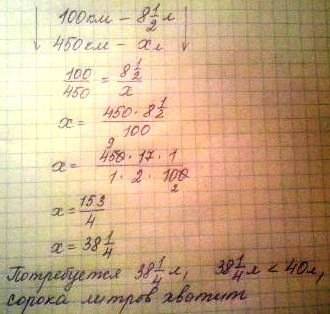
В решении.
Пошаговое объяснение:
1) (х - 4)(х + 2) > (x - 5)(x + 3)
x² + 2x - 4x - 8 > x² + 3x - 5x - 15
x² - 2x - 8 > x² - 2x - 15
x² - x² - 2x + 2x + 15 - 8 > 0
7 > 0, доказано.
Решение неравенства: х∈(-∞; +∞).
х может быть любым.
2) (m - 4)(m + 6) < (m + 3)(m - 1)
m² + 6m - 4m - 24 < m² - m + 3m - 3
m² + 2m - 24 < m² + 2m - 3
m² - m² + 2m - 2m - 24 + 3 < 0
-21 < 0, доказано.
Решение неравенства: m∈(-∞; +∞).
m может быть любым.
3) x² + 1 >= 2x
x² - 2x + 1 >= 0
Приравнять к нулю и решить как квадратное уравнение:
x² - 2x + 1 = 0
D=b²-4ac =4 - 4 = 0 √D=
0
х=(-b±√D)/2a
x=2/2
x=1.
Такое решение квадратного уравнения показывает, что парабола не имеет точек пересечения с осью Ох, парабола "стоит" на оси Ох в точке х = 1, весь график расположен над осью Ох.
Поэтому х может быть любым.
Решение неравенства: х∈(-∞; +∞).
А при х = 1 x² + 1 >= 2x, доказано.
1236
а) 85+7,8+98
б)4,7-17+7,5
в)64-90-100
г)-80+16+84
д)-a+m-2,6
е)c-a-b
ж)a-b+k+n
з)-a+b-c
и)m-n-p+k
1237
а)5,4+3,7-5,4=3,7
б)-8,79-1,76-8,79=15,82
в)3,4+2,9-3,4+4,1=7
г)4,67-3,94+3,94-3,67=1
д)7,2-3,2+5,9=9,9
е)4,8+2,75-4,8+3,25=6
ж)-6,9-4,21+10,9=-021
з)3,72-5,43-4,57-3,22=-9,5
Пошаговое объяснение:
В обычных примерах: если перед скобкой стоит знак минус, то у чисел в скобке меняется знак на противоположный
Дроби: приводим к общему знаменателю; числитель умножаем на то же число, что и знаменатель; записываем как общую дробь, где один знаменатель и 3 (в данном случае) числителя; вычисляем числитель; сокращаем дробь