Стародавні греки встановили надзвичайно цікавий факт, що існує всього п’ять правильних опуклих многогранників різної форми (тетраедр, гексаедр, октаедр, додекаедр, ікосаедр).
Правильні многогранники, крім куба, мали невелике поширення в практиці. Вони рідко зустрічаються в архітектурі, у живопису, проте іноді вони стають у пригоді.
Наведемо приклад. Легко впевнитись, що вершини кожного з п’яти видів правильних многогранників, в тому числі й ікосаедра, лежать на кульовій поверхні. Дванадцять вершин ікосаедра – це максимальне число точок, які можна нанести на поверхню кулі так, щоб відстань між будь-якими двома сусідніми точками була однакова.
Цю властивість ікосаедра застосувала одна з американських фірм для виготовлення баскетбольних м’ячів. На поверхні сферичної основи встановили 12 точок, рівномірно розділених по каркасу (вершини ікосаедра). Машина намотує нейлонові нитки по колам великих кругів, які проходять через кожну пару зазначених точок. Коли таке намотування буде повторено багато разів, причому, починаючи щоразу з різних пар точок, камера буде покрита цілком рівномірно, що забезпечить однакову міцність кожного її квадратного сантиметра.
ответ: Максимум - (4;29), Минимум - (0;-3)
Пошаговое объяснение:
(Как я понимаю, ночью ставки выше)
Возьмем производную данной функции, чтобы затем найти экстремум:
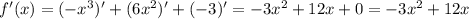
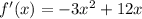
Известно, что производная принимает нулевое значение в точке экстремума ⇒ приравняв производную к нулю мы сможем его найти.
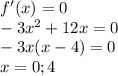
Рассмотрим знак производной до x = 0. При x = -1 производная отрицательна ⇒ функция убывает и при x = 0 минимум (можем так говорить, так как функция обычный куб). Затем производная становиться положительной и функция возрастает, пока x не становиться равен 4. Здесь достигается максимум. Потом производная становиться вновь отрицательной.
Значит:
При x = 0 - 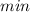
При x = 4 - 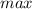
Подставим числа: