Пошаговое объяснение:
1. 1) 3ln |x| + C
2) ln |x+1| + C
2. 1) (x^4/4 + 2x^2 + x) | (1;2) = 2^4/4 + 2*2^2 + 2 - (1^4/4 + 2*1^2 + 1) = 4 + 8 + 2 - 1/4 - 2 - 1 = 10 3/4
2) e^x | (1;-1) = e^1 - e^(-1) = e - 1/e
3) sin x | (Π/2; Π/6) = sin Π/2 - sin Π/6 = 1 - 1/2 = 1/2
3. 1) Сначала находим пределы интегрирования
-x^2 + x + 6 = 0
-(x-3)(x+2) = 0
Пределы (-2; 3). Интеграл равен
-x^3/3 + x^2/2 + 6x | (-2;3) = -3^3/3 + 3^2/2 + 6*3 - (-(-2)^3/3 + (-2)^2/2 + 6(-2)) =
= -9 + 9/2 + 18 - 8/3 - 2 + 12 = 19 + 11/6 = 20 5/6
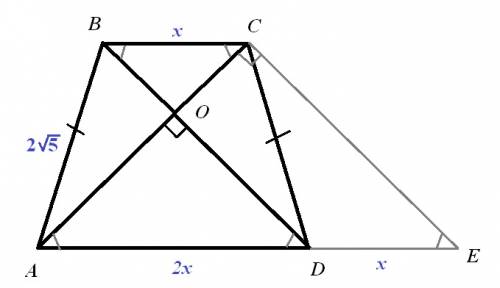
Чертеж во вложении.
1) Проведем через вершину меньшего основания прямую, параллельную диагонали - CЕ∥BD.
Диагонали равнобедренной трапеции равны и взаимно перпендикулярны. Получим равнобедренные прямоугольные треугольники:∆АОД, ∆ВОС, ∆АСЕ.
2) Пусть ВС=х, тогда по условию АД=2х.
В ∆ВОС по теореме Пифагора ВС²=ВО²+ОС², ВО=ОС,
х² = 2ВО²
ВО=х√2/2
В ∆АОД по теореме Пифагора АД²=АО²+ОД², АО=ОД,
(2х)² = 2АО²
АО=х√2
В ∆АОВ по теореме Пифагора АВ²=АО²+ОВ²,
(2√5)²=(х√2)²+(х√2/2)²
20=2х²+½х²
х² = 8
х=2√2
3) ∆АВО=∆СДЕ (ВС=ДЕ, АВ=СД, АС=СЕ).
АС=СЕ=АО+ОВ=х√2+х√2/2=(3х√2)/2=(3·2√2)·√2/2=6
Значит,