1)
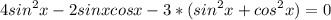
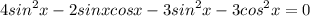
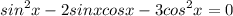
Т.к. уравнение однородное,то мы можем поделить уравнение на cos²x≠0

Пусть tgx = t, тогда


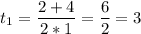

Вернёмся к замене
Если t = 3, тогда
tg x = 3
x = arctg(3)+пn, n∈Z
Если t = -1, тогда
tg x = -1
x = arctg(-1)+пn
x = -п/4 + пn, n∈Z
ответ: x = arctg(3)+пn, x = -п/4 + пn, n∈Z
2)
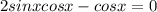
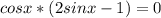
Произведение равно нулю,когда хотя бы один из множителей равен нулю
а) cos x =0
x = п/2 + пn, n∈Z
б) 2sin x - 1 = 0
sin x = 0,5
x = (-1)ⁿ*arcsin(0,5)+пn
x = (-1)ⁿ*п/6+пn, n∈Z
ответ: x = п/2 + пn, x = (-1)ⁿ*п/6+пn, n∈Z
3)
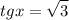
x = arctg(√3)+пn
x = п/6 + пn, n∈Z
ответ: x = п/6 + пn, n∈Z
4)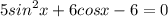



Пусть cosx = t, -1 ≤ t ≤ 1 тогда
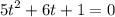
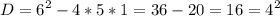


Вернёмся к замене
Если t = -0,2, тогда
cos x = -0,2
x = ±arccos(-0,2)+2пn, n∈Z
Если t = -1, тогда
cos x = -1
x = п + 2пn, n∈Z
ответ: x = ±arccos(-0,2)+2пn, x = п + 2пn, n∈Z
36 конфет было изначально в коробке
Пошаговое объяснение:
Пусть х конфет было изначально в коробке. Тогда:
х-4 конфет осталось в коробке, когда Таня взяла 4 конфеты
(х-4) - 1/4(х - 4) = х - 4 - 1/4х + 1 = 3/4х-3 конфет осталось в коробке, когда Таня взяла 1/4 часть оставшихся в ней конфет, что равно 2/3х всех конфет
Составим уравнение:
3/4х - 3 = 2/3х
3/4х - 2/3х = 3
(3*3-2*4)/12х = 3
1/12х = 3
х = 3 : 1/12
х = 3*12
х = 36 конфет было изначально в коробке
Проверим:
36 - 4 = 32 конфеты осталось в коробке, когда Таня взяла 4 конфеты
32 - 1/4*32 = 32 - 8 = 24 конфеты осталось в коробке, когда Таня взяла 1/4 часть оставшихся в ней конфет, что равно 2/3 всех конфет в коробке
24 = 2/3*36
24 = 24 - верно
|х|-2=2
|х|=2+2
|х|=4
х1=4;х2=-4
|8-0,2х|=12
8-0,2х=12
0,2Х=8-12
0,2х=-4/:0,2
х=-8