ДАНО
Y = (x² + 9)/x
ИССЛЕДОВАНИЕ
1. Область определения. Деление на ноль в знаменателе.
Х≠ 1.
Х∈(-∞;0)∪(0;+∞)
2. Вертикальная асимптота: Х= 1.
3. Пересечение с осью Х. Y(x) = 0 - нет.
4. Пересечение с осью У - нет
5. Наклонная асимптота
k = lim(+∞)Y(x)/x = 4*x/x = 4. Уравнение асимптоты: Y = 4*x.
6. Проверка на чётность.
Y(-x) ≠ Y(x). Y(-x) ≠ - Y(x)
Функция ни четная ни нечетная.
7. Поведение в точке разрыва.
lim(->0-) Y(x) = -∞.
lim(->0+) Y(x) = +∞
8, Первая производная.
6. Локальные экстремумы.
Y'(x) = 0, x1 = - 3/2, x2 = 3/2
Максимум Y(-3/2)= .-12.
Минимум Y(3/2) = 12.
7. Участки монотонности функции.
Возрастает - Х∈(-∞;-3/2]∪[3/2;+∞).
Убывает - Х∈[-3/2;0)∪(0;3/2]
8. Вторая производная.
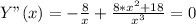
Корней нет. Точек перегиба (на графике) - нет.
9. Выпуклая - "горка" - Х∈(-∞;0). Вогнутая - "ложка" - Х∈(0;+∞)
10. График в приложении

1.а) 2/5, что составляет 2/5*100-=40% ; б)75/50=3/2, что составляет 3/2*100=150%; в) 7/20, что составляет 7/20=35%; г)40/32=1,25, что составляет 1,25*100=125%.
2. Осталось 620-200=420 г сыра, что составляет 420/600=21/30 часть всего сыра.
3, а).Лисичек будет 123-45=78, что составляет 78/123=26/41 часть от всех грибов.
3. Обозначим искомое число через x.Тогда 2/3 от х равно 2/3*х (две третих, умноженное на х).Обозначим эту часть через у, то есть у=2/3*х. Но по условию 1/3 от у равна 6, то есть 1/3*у=6.Подставим вместо у выражение: 1/3*2/3*х=6. Отсюда 2/9*х=6, х=9/2*6=27.
15:5=3
Это значит, что в длину будет по 4 сто