Пошаговое объяснение:
а) 4,8,12,16…;
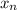 =4n
=4n
б) 1,-1,1,-1….
 =
=
2. Последовательность задана в аналитической форме yn=2n+10
Найти 10,50,63 член последовательности.
y₁₀=2·10+10=30
y₅₀=2·50+10=110
y₆₃=2·63+10=136
3. Последовательность задана в аналитической форме yn=n² +2.
Найти 5,10,13 член последовательности.
y₅=5²+2=25+2=27
y₁₀=10²+2=102
y₁₃=13²+2=171
4. Последовательность задана в рекурсивном виде y1=5
y n =y n-1 −3 , если n=2,3,4…
Найти 5,11,12 член последовательности.
y₅=y₄-3=y₃-3-3=y₂-3-3-3=y₁-3-3-3-3=y₁-4·3=5-4·3=-7
y₁₁=y₁₀-3=...=y₁-(11-1)·3=5-10·3=-25
y₁₂=y₁₁-3=...=y₁-(12-1)·3=5-11·3=-28
Это арифметическая прогрессия с разностью -3. Несложно доказать преобразуя данное рекурсивное соотношение
5. Последовательность задана в рекурсивном виде y 1 =3, y 2 =8 , y n =2y n-2 +3,
если n=3,4,5…. Найти 3,4,9 член последовательности.
y₃=2y₁+3=2·3+3=9
y₄=2y₂+3=2·8+3=19
y₅=2y₃+3=2·9+3=21
y₆=2y₄+3=2·19+3=41
y₇=2y₅+3=2·21+3=45
y₈=2y₆+3=2·41+3=85
y₉=2y₇+3=2·45+3=93
36
Пошаговое объяснение:
Чтобы решить задачу, посмотрим, как устроен еженедельник из задачи. Его конструкция точно такая же, как и обычной ученической тетради. Берется несколько листов бумаги, по оси симметрии сцепляются скобками, и полученная пачка сгибается пополам. В результате, на 1 исходном листе получается 4 страницы, причем левый полулист по счету с начала, будет такой же как и правый полулист по счету с конца (в обратном направлении).
В нашей задаче на листе встречаются страницы с номерами 14 и 23, значит на этом же листе есть страницы №13 и №24 (т.к. начинается нумерация страниц с нечетного числа и заканчивается чётным). Очевидно, что 14 - это левая часть листа - полулист под номером 14:2=7.
Значит правая часть листа будет седьмой с конца.
Значит осталось еще правых 6 полулистов до конца еженедельника.
6 полулистов это 6*2=12 страниц.
24+12=36
Значит страница №36 - последняя в еженедельнике и всего их 36.
Задача решается именно для такой конструкции еженедельника, как указано выше. Для клеенного издания условие не подходит. т.к. на одном листе там обязательно будут соседние страницы.
найдём одз: х не=0, т.к. на 0 делить нельзя;
(1/х+1)^2=4/4+5/4; извлекаем корень;
1/х+1=+-3/2;
а) 1/х=-2/2-3/2, 1/х=-5/2 |*2х, 2=-5х, х=-2/5,
х1=-0,4;
б) 1/х=-2/2+3/2, 1/х=1/2 |*2х, х=2,
х2=2.
умножим на х^2;
1+2х=5/4*х^2; умножим на 4/5;
х^2-2*4/5х-4/5=0;
х^2-2*4/5х+16/25-16/25-20/25=0;
(х-4/5)^2=36/25; извлекаем корень;
х-4/5=+-6/5;
а) х=4/5-6/5, х1=-2/5=-0,4;
б) х=4/5+6/5, х2=10/5=2.