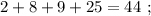![1)...= \{u=2x;\,\,\, du=2dx\}= \dfrac{1}{2} \int\limits { \dfrac{\cos u}{ \sqrt[3]{4-2\sin u} } } \, du= \\ \\ =\{4-2\sin u =t;\,\,\,\,-2\cos u\,\, du=dt\}=- \dfrac{1}{4} \int\limits { \dfrac{dt}{ \sqrt[3]{t} } }=\\ \\ =- \dfrac{3t^{ \frac{2}{3} }}{8} +C=- \dfrac{3}{8} \cdot \sqrt[3]{(4-2\sin u)^2} +C=- \dfrac{3}{8} \cdot \sqrt[3]{(4-2\sin 2x)^2} +C](/tpl/images/0707/4180/2cdaa.png)
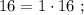
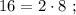
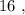т.е.: 
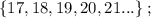
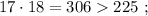
каждое – будет, очевидно, больше чем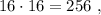 
т.е. больше 
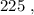а значит, при выборе минимальных чисел в виде 
и – подобрать остальные числа невозможно.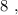
т.е.: 
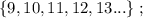
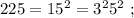
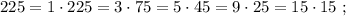
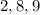и 
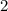и 
и 
Вася никаких чисел добавить не мог бы, поскольку тогда минимальные числа стали бы другими, и их произведение уже не было бы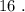 
и никаких натуральных чисел нет. и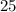 
Вася тоже никаких чисел добавить не мог бы, поскольку тогда максимальные числа стали бы другими, и их произведение уже не было бы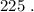 
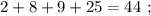
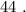
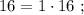
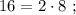
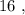т.е.: 
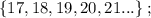
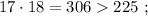
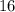каждое – будет, очевидно, больше чем 
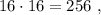т.е. больше 
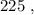а значит, при выборе минимальных чисел в виде 
и 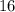– подобрать остальные числа невозможно.
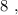т.е.: 
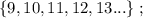
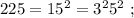
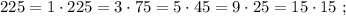
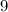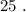
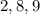и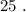 
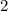и 
и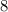 
Вася никаких чисел добавить не мог бы, поскольку тогда минимальные числа стали бы другими, и их произведение уже не было бы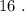 
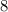и 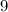никаких натуральных чисел нет. 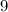и 
Вася тоже никаких чисел добавить не мог бы, поскольку тогда максимальные числа стали бы другими, и их произведение уже не было бы 
