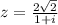
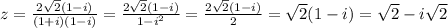
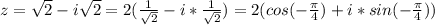
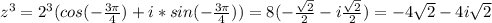
а)
Пошаговое объяснение:
Перевод: Который из выражений имеет смысл при любом значении х?
Решение. Если некоторое выражение имеет смысл при любом значении х, то область допустимых выражений совпадает с осью Ох. Последнее означает, что ОДЗ равен (-∞; +∞).
Поэтому определим ОДЗ каждого выражения:
а)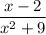 
- знаменатель x²+9≥9>0, поэтому ОДЗ: (-∞; +∞), то есть выражение имеет смысл при любом значении х;
б)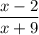 
- при x=-9 знаменатель рана 0, поэтому ОДЗ: (-∞; -9)∪(-9; +∞), то есть выражение имеет смысл не для любого значения х;
в)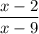 
- при x=9 знаменатель рана 0, поэтому ОДЗ: (-∞; 9)∪(9; +∞), то есть выражение имеет смысл не для любого значения х;
г)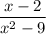 
- при x=±3 знаменатель рана 0, поэтому ОДЗ: (-∞; -3)∪(-3; 3)∪(3; +∞), то есть выражение имеет смысл не для любого значения х.
