Пошаговое объяснение:
Точка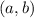 
на комплексной плоскости изображает число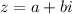 
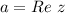- действительная часть числа (Real)
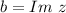- мнимая часть числа (Imaginary)
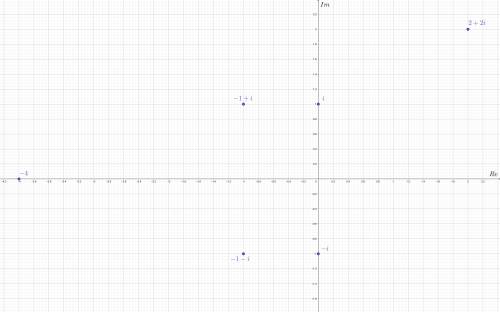
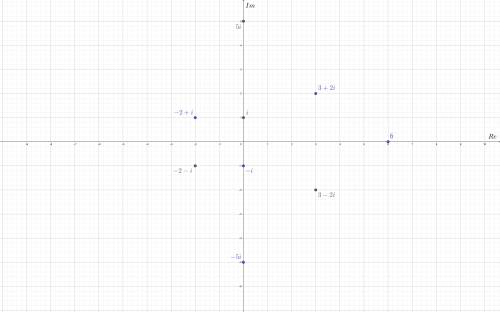
В соответствии с этим строим точки для 16.1. (Картинка 1)
Комплексно-сопряженные числа — пара комплексных чисел, обладающих одинаковыми действительными частями и равными по абсолютной величине противоположными по знаку мнимыми частями.
Т.е. сопряженным для числа 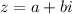будет являться число 
.
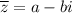В графическом представлении это означает, что сопряженное число будет являться отражением исходного числа относительно действительной оси (оси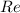 
).
На Картинке 2 серым обозначены исходные точки и синим - комплексно-сопряженные с ними.
var b,i,z,k: integer;
a: array[1..10000] of integer;
begin
read(b);
z: =0;
k: =0;
while b> 0 do
begin
z: =z+1;
a[z]: = b mod 10;
b: =b div 10;
end;
for i: =2 to z-1 do
if a[i]=a[i-1] or a[i]=a[i+1] then
k: =1;
if k=1 then writeln (‘да’)
else writeln (‘нет’);
end.
второй способ:
var a,b,c: integer;
begin
read(a);
k: =0;
c: =10; // это должно быть обязательно число, но не цифра
while a > 0 do
begin
b: =a mod 10;
a: =a div 10;
if b=c then k: =1;
c: =b;
end;
if k=1 then writeln (‘да’)
else (‘нет’);
end.
х=27+26 x=65-13
х=53 x=52
53-27=26 13+52=65