27.
Пошаговое объяснение:
Обозначим среднее из этих чисел буквой А, тогда меньшее число равно А-2, большее равно А+2, а их сумма равна утроенному среднему: 3А=87; А=29; А-2=27. При исследовании мы не записывали эти числа в виде 2n+1, как принято записывать нечетные числа, их нечетность получилась автоматически благодаря нечетности А (кстати, А ещё обязано делиться на 3) (если бы А было четным, его нельзя было бы представить в виде суммы трех последовательных нечетных чисел, а в виде суммы трех последовательных четных чисел можно, но естественно только при условии делимости А на 3).
На месте знака вопроса могло оказаться число 4 или 6
Пошаговое объяснение:
Разложим все числа на простые множители:
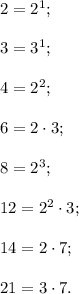
Таким образом, сомножитель 2 встречается 10 раз, сомножитель 3 — 4 раза, сомножитель 7 — 2 раза.
Количество троек равно количеству прямых линий, значит в каждой из них только одно число делится на 3.
Сомножитель 7 входит всего два раза на четыре прямых линии, значит одно из таких чисел находится на единственном пересечении трех из них (третий столбец слева на рисунке). Но это не может быть 21, так как иначе оно будет стоять в одном ряду с уже стоящим числом 3. Тогда в этом месте стоит 14.
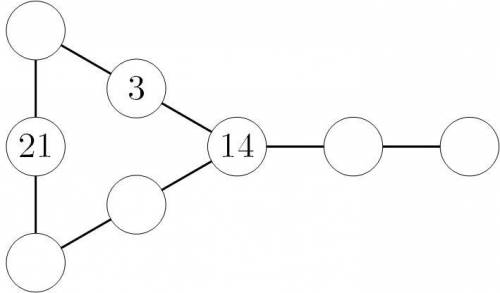
Значит 21 стоит в единственном возможном месте, помимо трех пересекающихся линий — посередине первого столбца.
Текущее положение — см. рис. 1.
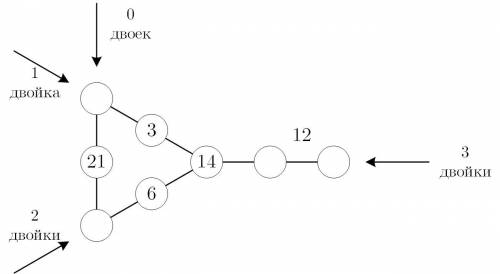
Пусть 6 стоит во втором столбце ниже 3. Тогда 12 стоит где-то справа от 14 и осталось расставить числа 2, 4 и 8.
Текущее положение — см. рис. 2.
Тогда в первый столбец можно поставить (сверху вниз) либо 4 и 2 (тогда справа от 14 будет 8 и это будет перебор), либо 8 и 4 (тогда справа от 14 будет 2, произведения сложатся кроме первого столбца, в котором будет пять двоек, в то время как в других линиях по четыре).
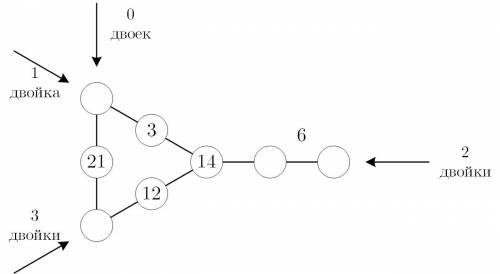
Значит предложенный вариант неправильный и во втором столбце ниже 3 стоит 12.
Текущее положение — см. рис. 3.
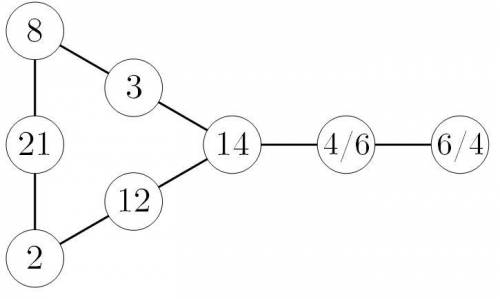
Тогда в первый столбец можно поставить (сверху вниз) 8 и 2, а справа от 14 — 4.
Числа 4 и 6 справа от 14 можно переставлять между собой, на результат они не повлияют.
Конечная расстановка указана на рис. 4.