Пошаговое объяснение:
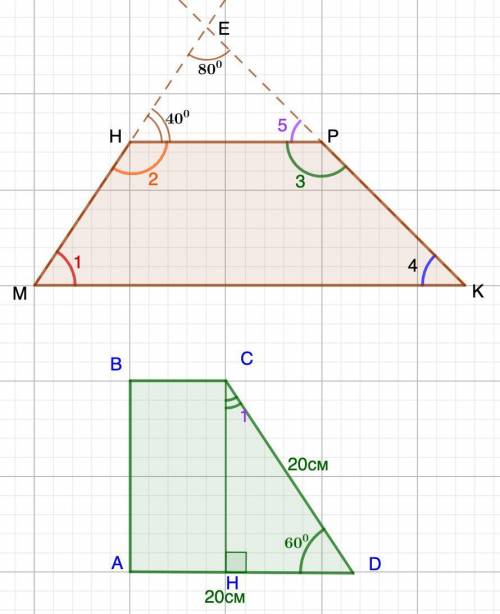
1. Дано: МНРК - трапеция.
МН ∩ РК = Е
∠МЕК=80°; ∠ЕНР=40°
Найти: углы трапеции.
1) Рассмотрим ΔНЕР.
Сумма углов треугольника равна 180°.⇒ ∠5=180°-(80°+40°)=60°
2) ∠ЕНР=∠1=40° - соответственные при НР║МК и секущей МЕ.
3)
Сумма смежных углов равна 180°.⇒ ∠2=180°-40°=140° - смежные.
4) ∠5=∠4 =60°- соответственные при НР║МК и секущей ЕК.
5) ∠3=180°-∠5=180°-60°=120° - смежные.
∠1=40°; ∠2=140°; ∠3=120°; ∠4=60°
2. Дано: АВСD - прямоугольная трапеция.
∠D = 60°;
АD=СD=20 см.
Найти: ВС.
1) Проведем высоту СН.
Рассмотрим ΔНСD - прямоугольный.
∠D = 60°
Сумма острых углов прямоугольного треугольника равна 90°.⇒ ∠1=90°-60°=30°.
Катет, лежащий против угла 30° равен половине гипотенузы.⇒ НD = СD:2=20:2=10 (см)
2) АН=АD-НD=20-10=10 (см)
3) Рассмотрим АВСН:
Если две прямые перпендикулярны третьей прямой, то они параллельны:СН⊥АD (построение)
АВ⊥АD (условие)
⇒ СН║АВ.
АВСН - параллелограмм.
Противоположные стороны параллелограмма равны.⇒ ВС=АН = 10 см.
Период - это число, которое в записи десятичной периодической дроби повторяется бесконечно.
1,6 - конечная десятичная дробь (одна целая шесть десятых)
1,6 = 1,6000... = 1,6(0) - можно записать в виде периодической дроби (но так не принято)
- - - - - - - - - -
1,666... = 1,(6) - бесконечная десятичная периодическая дробь (одна целая, шесть десятых в периоде)
- - - - - - - - - -
1,6457... - бесконечная непериодическая десятичная дробь
- - - - - - - - - -
1,30606... = 1,3(06) - бесконечная десятичная периодическая дробь (одна целая, три десятых, шесть тысячных в периоде)
-Салэм! Хэллерем яхшы
-Син буген нэрсэдэ кайтасын?
-Мин эти белэн машинада кайтам.
-Э синен этиеннен нинди машина?
-Минем этиемнен Рено Дастер. Э синен этиеннен?.
-Минем этиемнен Рено Сандера
-Ярар. Мин киттем.