ответ: х=12
45-х=12+21 ← ( вначале просто сложим что можем сложить..))
45-х=33 ← (( получили обычное уравнение. решаем ..)) ↓↓
х=45-33 ← (( решаем ))
х=12 ← (( ответ ))
Пошаговое объяснение: эти уравнения надо решать так: просто умножим или сложим, вычтем, а потом решаем как обычно...
(( могу немного подсказать или дать идею например: 45-х=33 тут трудно думать как и что делать.. можно подставить мысленно простые числа.. 4-х=2 тут нам легко! - х=4-2. также и с 45-х=33 х=45-43.
МАТЕМАТИКА ЭТО ПРОСТО! удачи в учёбе!
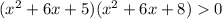
Метод интервалов.
Приравняем неравенство к нулю и найдем нули множителей:

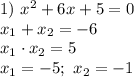
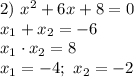
Перепишем многочлены вида 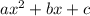 на множители вида
на множители вида 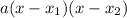 , где
, где 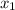 и
и 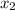 — корни квадратного уравнения
— корни квадратного уравнения 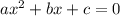
Имеем:
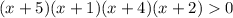
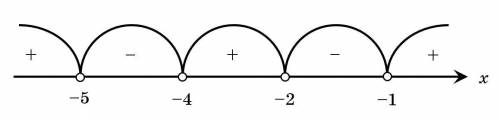
Начертим координатную прямую и отметим выколотыми точками (так как неравенство строгое) нули множителей, и определим знак на каждом интервале ("+", если на этом интервале функция 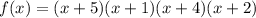 выше оси абсцисс, "–" — ниже оси абсцисс). См. вложение.
выше оси абсцисс, "–" — ниже оси абсцисс). См. вложение.
Следовательно, промежутками, на которых функция 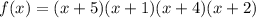 больше нуля (выше оси абсцисс), являются:
больше нуля (выше оси абсцисс), являются:
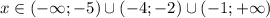
Неравенство вида 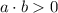 выполняется в двух случаях:
выполняется в двух случаях:
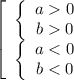
Следовательно, рассмотрим первый случай:
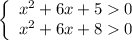
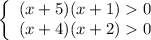
Здесь  и
и 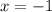 — точки пересечения графика функции
— точки пересечения графика функции 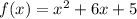 с осью абсцисс, и
с осью абсцисс, и 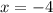 и
и  — точки пересечения графика функции
— точки пересечения графика функции 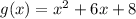 с осью абсцисс.
с осью абсцисс.
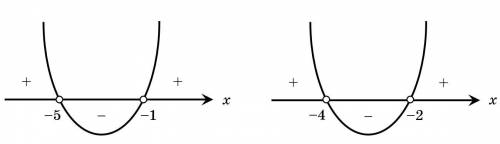
Изобразим две параболы для каждого неравенства и определим те абсциссы, при которых каждая из них больше нуля (см. вложение). Имеем промежутки:
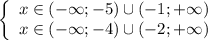
Следовательно, промежутками, при которых оба неравенства выполняются одновременно, являются:
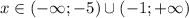
Рассмотрим второй случай:
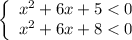
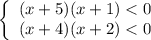
Из тех же парабол определим те абсциссы, при которых каждая из них меньше нуля:
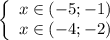
Следовательно, промежутком, при котором оба неравенства выполняются одновременно, является:
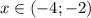
Объединим оба случая и получим решение неравенства:
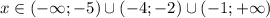
ответ: 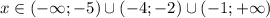
2)95-89=6
ответ 6 деталей осталось