Рассмотрим функцию 
. Тогда исходное уравнение имеет вид: 
.
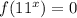Заметим, что любой положительный корень уравнения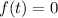 
однозначно определяет корень уравнения 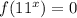(это верно в силу того, что уравнение 
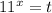(относительно 
) имеет ровно одно решение, так как показательная функция монотонно возрастает на своей области определения). Тогда переформулируем задачу.
При каких значениях параметра 
, уравнение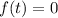 
имеет ровно один положительный корень?
График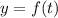 
представляет собой параболу с ветвями вверх.
Исследуем местоположение ее вершины.
.
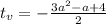Заметим, что при любом значении параметра , 
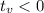(это следует из отрицательности дискриминанта). Это говорит о том, что либо у нас вообще нет корней (вершина находится выше оси абсцисс), либо у нас таки есть корень, но он обязательно будет отрицательным.
Для того чтобы мы имели положительный корень, необходимо и достаточно потребовать следующее условие: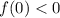 
.
Тогда имеем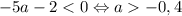 
.
ответ: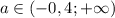 
.
16:2=8- чётных чисел.
8+3=12(задач) решила Маша.
сколоко задач решила Маша, если после проверки 2 Машины задачи оказались неправильтными? (12-2=10(задач))
сколько получила маша, если за 5 первых заданий она получила по 1у за задание, а остальные задания по 2? 1)5*1=5(з.)-за 1е 5 задан. 2)10-5=5 (заданий) по 2б. 3)5*2=10 (б.) за 5 заданий. 4)5+10=15(Б) ПОЛУЧИЛА МАША
сколько времени Маша решала задания, если 1е 3 задания она решила по 2 минуты каждую, а остальные по 8 минут каждую. (всего она решила 10.) 1)3*2=6(минут) за первые три задания. 2)10-3=7(задан.)- по 2 минуты каждая. 3)2*7=14минут она затратила на остальные задачи. 7+14=21(мин.)
- 58 + х - 41,3 = 6,287
х = 6,287 + 41,3 + 58
х = 105,587
Проверка :
- (58 - 105,587) - 41,3 = 6,287
- (- 47,587) - 41,3 = 6,287
47,587 - 41,3 = 6,287
6,287 = 6,287