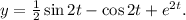
Пошаговое объяснение:
Имеем дело с неоднородным линейным уравнением с постоянными коэффициентами. Стандартный прием: искомое решение представляется в виде суммы решения однородного уравнения и частного решения неоднородного: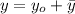 
.
Однородное уравнение: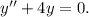 
Характеристическое уравнение имеет следующий вид: 
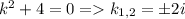. Тогда решение однородного уравнение можно записать в виде: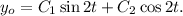 
Так как в правой части исходного уравнения перед экспонентой стоит многочлен нулевой степени, а коэффициент в показателе экспоненты не совпадает с каким-либо корнем характеристического уравнения, то частное решение можно искать в виде: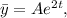 
подставим его в исходное уравнение и найдем коэффициент 
:
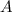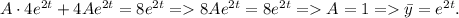
Значит, общее решение исходного уравнения есть
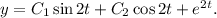Осталось определить коэффициенты для данной задачи Коши:
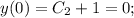
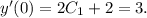
Решая каждое из этих уравнений, находим: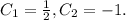 
В итоге, получаем ответ:
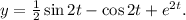
Пошаговое объяснение:
все задачи решаются из прямоугольного треугольника, образованного наклонной гипотенуза), перпендикуляром из точки наклонной (катет) и проекцией наклонной на плоскость (катет)
наклонная - L, перпендикуляр -h, проекция - а
1) h - это катет напротив угла в 30°, значит он вдвое меньше гипотенузы ⇒ L= 2h = 20cм
2) если угол 45°, значит треугольник равнобедренный - катеты равны ⇒ a = h = 4 см
3) перпендикуляр - это катет напротив угла 30°, значит он вдвое меньше гипотенузы h = 1/2 L = 6 см
и остаток от каждого куска "к" метров
тогда
а-а*0,2=к
0,8а=к
значит первый кусок:
а=к:0,8
аналогично
в-1/3в=к
2/3в=к
в=3/2к
с-7/15с=к
8/15c=к
c=15/8к
зная общую начальную длину:
a+b+c=222
k:0.8+3/2k+15/8k=222
k(10/8+3/2+15/8)=222
k((10+3*4+15)/8)=222
k*37/8=222
к=222*8/37=48 м оставалось от кусков
48:8=60 м кусок а
48*3/2=72 м кусок b
48*15/8=90 м кусок с
60+72+90=222 м