
Пусть высота цилиндра – х, тогда радиус основания цилиндра х+1
Диаметр вдвое больше радиуса, тогда диаметр 2*(х+1)=2х+2
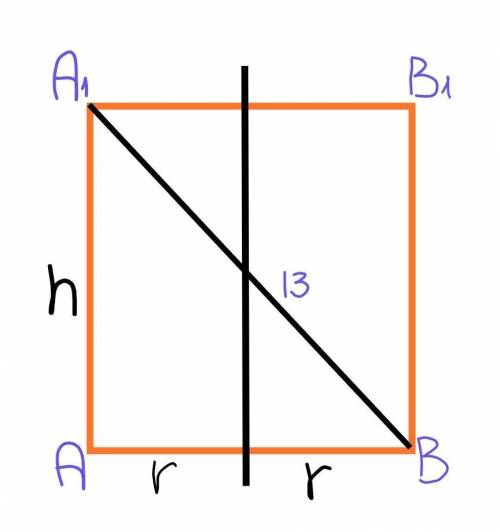
А1В1ВА – осевое сечение цилиндра, так как плоскость А1В1ВА проходить через ось цилиндра.
АВ – диаметр основания цилиндра, тогда АВ=2х+2
АА1 – высота цилиндра, тогда АА1=х
Рассмотрим ∆А1АВ.
Угол А1АВ – прямой, так как АА1 – высота, следовательно ∆А1АВ – прямоугольный с прямым углом А.
В прямоугольном треугольнике А1АВ по теореме Пифагора:
А1В²=АА1²+АВ²
13²=х²+(2х+2)²
169=х²+4х²+8х+4
5х²+8х–165=0
Д=8²–4*5*(–165)=64+3300=3364
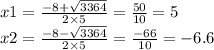
Так как длина задаётся положительным числом, то высота равна 5.
Тогда радиус основания цилиндра равен 5+1=6.
Sосн.=r²*π=6²π=36π
Sбок.=2πrh=2π*6*5=60π
Sпол.=2*Sосн.+Sбок.=2*36π+60π=72π+60π=132π
V=πr²h=6²*5π=36*5π=180π
ответ: 1А; 2Д; 3Г; 4Б
В четвертом классе многих детей и родителей пугают задачи на движение. Сегодня мы поделимся, как одно небольшое изменение подачи формулы, может научить ребенка щелкать подобные задачи, словно орешки.
В школе, по традиционной программе, детей знакомят с формулой в линейной структуре, записывая ее на доске и поясняя S=v*t
Опытный учитель не только расскажет, что S — расстояние v — скорость t — время, а обязательно объяснит, почему обозначение происходит именно такими буквами.
Дальше ребенку последовательно предлагается блок задач, сначала на применение прямой формулы S=v*t
Потом обратной. V=S:t t=S:v
Конечно ребенку нужно будет выучить правило нахождения расстояния, времени или скорости. Правила с одной стороны, очень понятны взрослым, с другой очень трудны для детей.
Потому что читая задачу, маленький ученик, который только учится решать задачи, в голове прокручивает алгоритм:
1. Известно, что …
2. Надо узнать…
3. Чтобы ответить на вопрос, надо … (тут происходит процесс определения нужной формулы, обычно это самая трудная часть)
4. Можем сразу ответить на вопрос? Нет. Сразу мы не можем ответить на вопрос задачи, так как не знаем…
5. Поэтому в первом действии мы узнаем …
6. Во втором действии мы ответим на вопрос задачи. Для этого …
Сложный алгоритм, но именно так решают задачи младшие школьники! Некоторые делают это очень быстро, а некоторые продумывают каждый шаг.