Пошаговое Сначала нужно вынести за скобки общий знаменатель, который есть у каждого произведения. После этого найти значение в скобках. Для этого необходимо правильную дробь перевести в неправильную и избавиться от целой части дроби, полученный результат умножить на значение за скобками, предварительно сократив числитель и знаменатель дроби.
3/4 * 1 1/15 + 1 1/15 * 2 1/2 - 1 3/8 * 1/15 = 1 1/15 * (3/4 + 2 1/2 - 1 3/8) = 1 1/15 * (3/4 + 5/2 - 11/8) = 1 1/15 * (3 * 6 + 5 * 12 - 11 * 3)/24 = 1 1/15 * (18 + 60 - 33)/24 = 1 1/15 * 45/24 = 16/15 * 15/8 = 2 .
ответ: 2.объяснение:
1) 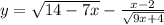
Область определения этой функции должна удовлетворять двум условиям:
1) подкоренное выражение неотрицательно (т.е. 14 - 7х ≥ 0 и 9х + 4 ≥ 0)
2) знаменатель дроби отличен от нуля (т.е.  )
)
Поэтому эти условия удобно записать в виде системы:

Решением системы неравенств будет множество, которое и есть область определения функции.
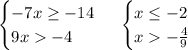
![x\in(-\frac{4}{9};\ 2]](/tpl/images/0525/6406/397dd.png)
ответ: ![(-\frac{4}{9};\ 2]](/tpl/images/0525/6406/39742.png)
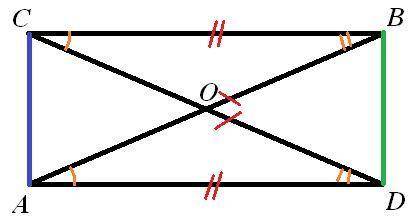
2) Рисунок к задаче - во вложении.
Проведем отрезки BD и AC.
Получим, что ΔABD=ΔCDB по трем сторонам (BD-общая, CB=AD, CD=AB) и ΔCDA=ΔABC по трем сторонам (AC-общая, CB=AD, CD=AB).
Из равенства ΔABD и ΔCDB следует, что соответственно равны ∠A и ∠C.
А из равенства ΔCDA и ΔABC следует, что соответственно равны ∠D и ∠B.
Наконец, рассмотрим ΔCOB и ΔAOD. У них CB=AD, ∠A=∠C, ∠В=∠D. Значит, ΔCOB = ΔAOD по стороне и прилежащим к ней углам.
Из равенства ΔCOB и ΔAOD следует равенство соответственных сторон СО и AO.
Доказано.

46,69
55,903
9,885
3.516
х-0.07=1.5
х=1.5+0.07
х=1,57
9-х=1.5
-х=1.5-9
-х=-7.5
х=7.5