ответ: Площадь 4,5
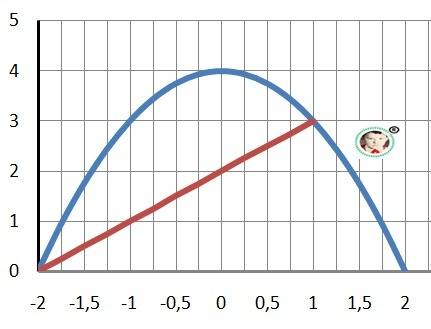
Дано: y = 4 - x²- парабола, y = x+2 - прямая
Найти: S=? - площадь фигуры
1) Находим точки пересечения графиков. - у1 = у2.
-x²-x+2=0 - квадратное уравнение
a = 1- верхний предел, b = -2- нижний предел.
2) Площадь - интеграл разности функций.
f(x) = 2-x- x² - подинтегральная функция - записываем в обратном порядке.
3) Интегрируем функцию и получаем:
F(x) = 2*x -1/2*x² - 1/3*x³
4) Вычисляем на границах интегрирования.
S(а) = S(1) = 2+-0,5-0,333 = 1,167 (1 1/6)
S(b) = S(-2) =-4+-22,667 = -3,333 (3 1/3)
S = S(a) - S(b) = 4,5 - площадь - ответ.
Рисунок к задаче в приложении.
Sполн=1032 см²
V=1512 см3
Пошаговое объяснение:
V=Sосн*H
S oсн=√ (p * (p-a) * (p-b) * (p-c))
p=P/2. P=a+b+c
p = (10+17+21) / 2
p=24
S=√ (24 * (24-10) * (24-17) * (24-21))
S=84
V=84*18
Площадь боковой поверхности треугольной призмы будет:
Sбок=18*(10+17+21)=864 см²
Для нахождения площади основания можно воспользоваться формулой Герона для нахождения площади треугольника, когда известны только длины его сторон, но неизвестна высота:
S=√p(p-a)(p-b)(p-c) (под корнем всё выражение!), где a,b,c- стороны треугольника, p- полупериметр треугольника, p=(a+b+c)/2.
p=(10+17+21)/2=24
S=√24(24-10)(24-17)(24-21)=√24*14*7*3=√7056=84 см²
Полная поверхность призмы равна:
Sполн=Sбок+2Sосн
Sполн=864+2*84=864+168=1032 см²
Sполн=1032 см²
1) 0,164 + 0,072 =0,232 (т)-собрал 2 класс
2) 0,164 +0,232=0,356(т) - собрали два класса вместе
ответ: два класса собрали вместе 0,356 т.