точка A(1;-2) расположена вне окружности
Пошаговое объяснение:
Решим задание через определение степени точки относительно окружности
Степенью точки относительно данной окружности называется разность

d — расстояние от точки до центра окружности,
R — радиус окружности.
Точки имеют следуюющие степени в зависимости от расположения:
- вне окружности - положительную,
- внутри окружности - отрицательную,
- на окружности - нулевую.
Общее уравнение окружности задается уравнением
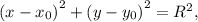
где (х0, у0) - координаты центра окружности
R - ее радиус.
В нашем случае:
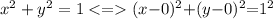
Следовательно,
радиус окружности R = 1;
центр окружности O = О(0; 0)
Теперь вычислим степень точки A(1;-2) относительно этой окружности:

Итак мы выяснили, что d² - R² > 0 =>
=> точка A(1;-2) расположена вне окружности.
Вариант 1.
1. Кефир = 3600/3=1200
Ряженка = 6000-(3600+1200)=1200
ответ:1200
2. (4946+2947):9=877
5*(125+75):20+80=130
(20498-13597)*7=48307
3. 6т 20 кг< 6 т 2 ц
20км 300м<23000м
3сут 10ч<90ч
400ц>4т
4.
3х=87-6
3х=81
х=27
290+х=640-260
х=640-260-290
х=90
5. Длина =9
Ширина =4
Площадь = 36см^2
Вариант 2.
1.груши =1200кг
Сливы =400 кг
2. (4760+1988):7=964
156-96:(12:4)*2=92
(80 035- 74 942)*6=30 558
3. 5км4м=5км40дм
95ч<4сут5ч
6т200кг<62000кг
3т<300ц
4.
84/х=42
х=84/42
х=2
400-х=275+25
400-х=300
х=100
5.ширина 4см
Длина 8 см
Площадь = 32см^2
Пошаговое объяснение:
Выражаем площадь как 3х*4х=>получаем 12х²
Подставляем: 192=12х²; х²=16, отсюда х1=4, х2=-4(не соотв. усл.)
То есть стороны равны 12 и 16
Ищем диагональ по теореме Пифагора:
d=√256+144=√400=20