n<arccos(R₁/R₂)/180
Пошаговое объяснение:
вероятность и геомтрия.
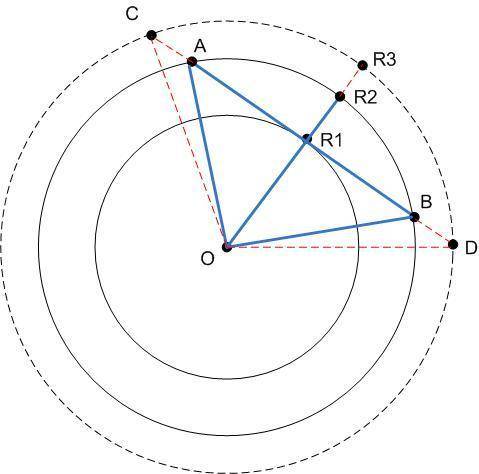
Посмотрим на рисунок. Назовем событие благоприятным, если точки А и В попадают (одновременно) в сегмент большой окружности AR₂B. Причем нарисованный вариант - имеет максимальную длину дуги (при данных величинах радиусов R₁ R₂), опирающуюся на хорду lABl, еще не пересекающую малую окружность ( lABl только касается меньшей окружности в т R₁).
Вопрос: в каких единицах будем измерять благоприятные (да и все возможные случаи)? В количестве точек - не реально. Точек, что на вышеуказанной дуге, что на всей окружности бесконечно много. Раз в количестве тчек не получается, то будем сравнивать длины дуг!
Итак вероятность n непересечения будет равне:
n=l₀₁/l₀₀, где
l₀₁ - длина дуги AR₁B (количество благоприятных случаев)
l₀₀ - длина большой окружности (количество всех возможных случаев)
С l₀₀ все просто:
l₀₀=2πR₂
Вычислим длину "благоприятной" дуги l₀₁ .
Дуга AR₂B опирается на центральный угол AOB. Найдем этот угол.
Рассмотрим Δ OAR₁. Этот треугольник прямоугольный (прямой угол ∠R₁, т.к. lABl -касательная к малой окружности в т.R₁).
Катет lOR₁l=R₁ (радиусу малой окружности), гипотенуза lOAl=R₂ - радису большой окружности.
lOR₁l/ lOAl=R₁/R₂=cos(∠AOR₁).
∠AOR₁=arccos(R₁/R₂) ⇒ ∠AOB=2*arccos(R₁/R₂).
Длина дуги AR₂B:
l₀₁=2*arccos(R₁/R₂)*2πR₂/360=arccos(R₁/R₂)*2πR₂/180 (запишем так для наглядности);
n=l₀₁/l₀₀, ⇒ n = (arccos(R₁/R₂)*(2πR₂)/(180) : 2πR₂) =arccos(R₁/R₂)/180;
n=arccos(R₁/R₂)/180. (1)
Замечание:
На рисунке есть еще одна окружность с радиусом R₃>R₂>R₁. Исходя из этого рисунка наблюдаем динамику роста "благоприятного" сектора при увеличении радиуса бОльшей окружности.
Проверка:
Подставим в полученную формулу отношение R₁/R₂=0,01 (R₂>>R1).
Посчитаем вероятность:
n=arccos(0,01)/180≈0,497.
Т.е. при росте "большой" окружности растет и длина "благоприятного" сектора, и в пределе этот сектор становится равным 1/2 длины окружности (вероятность становится равной 0.5 или 50%).
Справедливости ради формулу (1) надо записать вот так:
n<arccos(R₁/R₂)/180,
т.к. знак "=" - это предельный случай, точка касания, а не пересечения.
ответ: 0,96 а