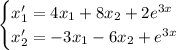
Дифференцируем первое уравнение:
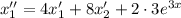
Подставим выражение для 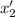 :
:
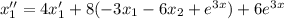
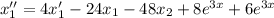
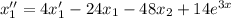
Домножим первое уравнение системы на 6 и сложим его с полученным уравнением:
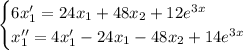
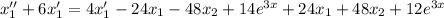
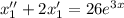
Составим однородное уравнение, соответствующее данному неоднородному:

Составим характеристическое уравнение:
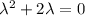
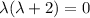
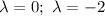
Общее решение однородного уравнения:
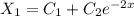
Частно решение неоднородного уравнения ищем в виде:
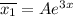
Найдем первую и вторую производную:
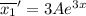
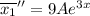
Подставим в неоднородное уравнение:
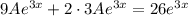
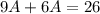
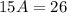
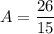
Частное решение неоднородного уравнения:
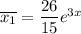
Общее решение неоднородного уравнения:
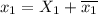
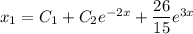
Найдем первую производную:
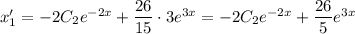
Выразим из первого уравнения 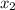 :
:
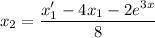
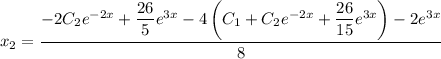
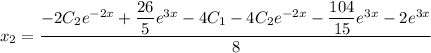
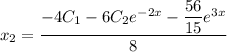
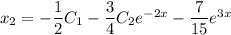
Общее решение системы:
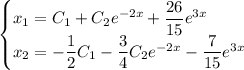
в 3 номере под а):
показатели корней разные (12 и 6), мы можем получить одинаковые, умножив показатель 6 на 2, поэтому и подкоренное выражение домножаем на 2:
было: √6ой степени из 5⁵, стало: √12ой степени из 5¹⁰
то же самое в номере 3 под б):
показатели корней разные (квадратный корень из 3 и кубический корень из 9), мы можем получить одинаковые, домножив квадратный корень на 3 (чтобы получить 6) и кубический корень на 2 (чтобы получить 6), поэтому и подкоренные выражения домножаем на 2:
было: √2ой степени из 3, стало: √6ой степени из 3³ и второй множитель: было: √3ей степени из 9, стало: √6ой степени из 9²
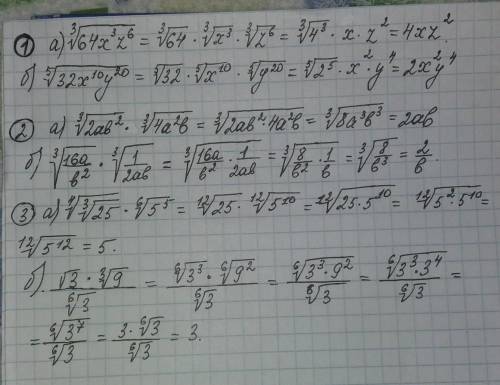
г) 7 4/4 - 3 3/4 = 4 1/4
е) 6 3/3 - 1 2/3 = 5 1/3
я не стала списывать начальный пример