18 карточек
Пошаговое объяснение:
Найдём количество чисел которые делятся на 2 с арифметической прогрессии.
Пусть a₁ = 10, aₙ = 48, d = 2 и нам необходимо найти n
Воспользуемся формулой: aₙ = a₁ + (n-1)·d
Выразим из этой формулы n:
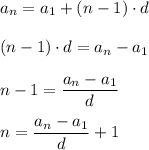
Подставим известные данные и найдём n:

Значит в данном наборе содержится 20 чисел, которые делятся на 2
Количество чисел которые делятся на 7 в данном наборе не так много и их можно просто перечислить.
На 7 делятся числа 14, 21, 28, 35, 42 и 49 - всего 6 чисел.
Но числа 14, 28 и 42 мы уже учли, так как они делятся на 2.
Поэтому количество чисел, которые делятся на 2 или 7 равно:
20 + (6 - 3) = 20 + 3 = 23 числа
Следовательно, количество чисел, которые не делятся на 2 или 7 равно 40 - 23 = 17 чисел
Мы можем взять не глядя 17 карточек, но все числа на них могут не делиться на 2 или 7, но если мы возьмём ещё как минимум одну карточку, то мы найдём как минимум одно число, которое делится на 2 или 7.
1 картинка: 46,6048
2 картинка: 113,04
Пошаговое объяснение:1 картинка:Площадь окружности равна 2π · r²(Для сокращения буду писать So)
Площадь прямоугольника ab(a и b - стороны)(S)
Площадь заштрихованной фигуры равна S-So
So=2π · r²=2π · 2,2²=2 · 3,14 · 4,84=6,28 · 4,84=30,3952
S=ab=7 · 11=77
S-So=77 - 30,3952=46,6048
2 картинка:(Я правильно понимаю, что эти окружности имеют общий центр?)
Обозначим радиус большей окружности R, а меньшей r
R=r + 3=1,5 + 3=4,5
Площадь окружности 2π·r²(Буду писать S для площади большей из окружностей, а s для площади меньшей)
Площадь заштрихованной фигуры S-s
S=2π · R²=2 · 3,14 · 4,5²=2 · 3,14 · 20,25=6,28 · 20,25=127,17
s=2π · r²=2 · 3,`14 · 1,5²=2 · 3,14 · 2,25=6,28 · 2,25=14,13
S-s=127,17 - 14,13=113,04
1/5 · 3/7 = 3/35
1/5 + 3/7 = 22/35
1/5/- 3/5 = 2 /35