ответ: 5 и 17.
Обозначим искомые числа за x и y. Тогда: x + y = 22.
Если сумма двух чисел - это четное число, то оба числа были одной и той же четности (то есть либо оба нечетные, либо оба четные).
Но и разность чисел одной четности - это тоже четное число. Поэтому x - y - это обязательно четное число. Но среди чисел меньше 14 и больше 10 только одно четное число, это 12 (считаем, что разность не может быть равна 10 и 14).
Тогда мы можем составить и решить эту систему уравнений:
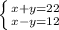
Сложим эти уравнения:
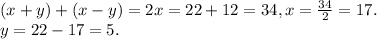
Получается, Сережа загдал числа 5 и 17.
Примечание.
Если же все-таки сумма может быть равна 10 и 14, то роме этой пары еще подойдут пары (19, 5) и (17 и 7).
2) разность уменьшиться на 7,6
3) разность уменьшиться на 12,2
4) разность увеличится на 17,96
5) разность увеличится на 0,1 (0,4 - 0,3 = 0,1)
6) разность увеличится на 4 (2,3 + 1,7=4)
7) разность уменьшиться на 9,5 (6,1+3,4=9,5)