Тело, которое получилось, имеет веретенообразную форму: два конуса с одним общим основанием,
радиусr которого - высота ВО треугольника АВС, проведенная к стороне АС, вокруг которой треугольник вращается;
образующие - АВ и ВС соответственно;
высота каждого конуса - СО и ОА, сумма которых равна АС.
Объем тела вращения равен сумме объемов конусов:
V=v₁ +v₂
v₁=Sh₁:3=πr²h₁:3
v₂=Sh₂:3=πr²h₁:3
V=πr²h₁:3+πr²h₁:3=S(h₁+h₂):3=πr²*АС:3
Радиус r основания, общего для обоих конусов, найдем из площади треугольника АВС, найденной по формуле Герона.
Вычисления банальны, приводить поэтому иx не буду.
Площадь треугольника АВС равна 84
r=ВО=2S ᐃ АВС:АС=168:21=8
V =πr²*АС:3=π*64*21:3=448π
Площадь поверхности равна сумме площадей боковой поверхности конусов:
Sт.вр.=πrL₁+πrL₂=πr(L₁+L₁)
Sт.вр.=π*8*(10+17)=216π
1)

Проверка:
0² - 25 · 0 = 0 25² - 25 · 25 = 0
0 - 0 = 0 25² - 25² = 0
0 = 0 0 = 0
2)
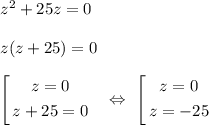
Проверка:
0² + 25 · 0 = 0 (-25)² + 25 · (-25) = 0
0 + 0 = 0 25² - 25² = 0
0 = 0 0 = 0
3)

Проверка:
0² - 1,7 · 0 = 0 1,7² - 1,7 · 1,7 = 0
0 - 0 = 0 1,7² - 1,7² = 0
0 = 0 0 = 0