Пошаговое объяснение:
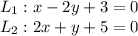
найдем точку пересечения прямых. для этого решим систему уравнений
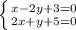
из первого выразим х х= 2у-3
подставим во второе 2(2у-3)+у+5=0; 4у -6 +у +5 =0; 5у=1; у=0,2
тогда х = 2*0,2 -3 = 0,4 -3 = -2,6
это наша точка пересечения М(-2,6; 0,2)
теперь уравнение прямой, параллельной оси оу
направляющий вектор оси оу s=(0;1), можем его использовать в качестве направляющего вектора искомой прямой, т.к. они параллельны
тогда каконическое уравнение прямой, проходяшей через точку М(-2,6; 0,2) параллельно оси оу будет
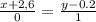
перейдем к обшему виду и получим
х = -2,6
х=5,2+3,2
х=8,4
-3,2+8,4=5,2
5,2=5,2
6,7+у=-4,3
у=-4,3-6,7
у=-11
6,7+ (-11)=-4,3
-4,3=-4,3
5,7-х=8,9
-х=8,9-5,7
-х=3,2
х=-3,2
5,7- (-3,2)=8,9
8,9=8,9
(х-6,8)+9,3=1,7
х-6,8=1,7-9,3
х-6,8=-7,6
х= -7,6+6,8
х=-0,8
(-0,8-6,8)+9,3=1,7
1,7=1,7