1.1)выполни с обьяснением: 812346 379254 423516 2) выполни указанные действие: 591328 167831 450839 709024 95 760: 7: 30 78 480: 6: 40. образец к 1 : 769 × 24 3076 +1538 18456 2.вычесли с обьяснением: 254307 481360. 3.456803 605102 528330 105420 521180 907*203 (180 876+251 367): 9 (580 000-35 410): 90 (634 100-17 300): 300 оброзец к 2 и 3 : 327 ×406 1962 +1308 132762

👇

Увидеть ответ

Ответ:

Ксения61831378

18.04.2020

Слишком долго...
1) 812
·346

4872
3248
2436

280952

379
·254

1516
1890
758

96216

423
·516

2538
423
2115

218268

4,7(33 оценок)

Открыть все ответы

Ответ:

Nikalusha

18.04.2020

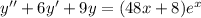
y''+6y'+9y=(48x+8)e^x

Общее решение неоднородного дифференциального уравнения равно сумме общего решения однородного дифференциального уравнения, соответствующего данному неоднородному, и частного решения неоднородного дифференциального уравнения.

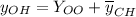
$y_{OH}=Y_{OO}+\overline{y}_{CH}$

Решим однородное дифференциальное уравнение, соответствующее данному неоднородному:

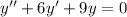
y''+6y'+9y=0

Составим и решим характеристическое уравнение:

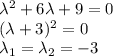
$\lambda^2+6\lambda+9=0\\(\lambda+3)^2=0\\\lambda_1=\lambda_2=-3$

Запишем общее решение однородного уравнения:

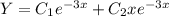
$Y=C_1e^{-3x}+C_2xe^{-3x}$

Частное решение будем искать в виде:

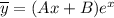
$\overline{y}=(Ax+B)e^x$

Найдем первую и вторую производную:

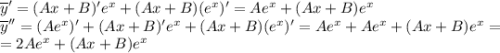
$\overline{y}'=(Ax+B)'e^x+(Ax+B)(e^x)'=Ae^x+(Ax+B)e^x\\\overline{y}''=(Ae^x)'+(Ax+B)'e^x+(Ax+B)(e^x)'=Ae^x+Ae^x+(Ax+B)e^x=\\=2Ae^x+(Ax+B)e^x$

Подставим значения функции и первых двух производных в исходное уравнение:

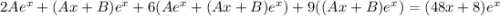
2Ae^x+(Ax+B)e^x+6(Ae^x+(Ax+B)e^x)+9((Ax+B)e^x)=(48x+8)e^x

Сократим на 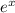e^x :

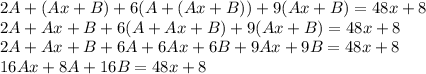
$2A+(Ax+B)+6(A+(Ax+B))+9(Ax+B)=48x+8\\2A+Ax+B+6(A+Ax+B)+9(Ax+B)=48x+8\\2A+Ax+B+6A+6Ax+6B+9Ax+9B=48x+8\\16Ax+8A+16B=48x+8$

Так как левая и правая часть равны, то коэффициенты при х и свободные члены также равны. Получаем систему:

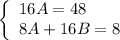
$\left\{\begin{array}{l} 16A=48 \\ 8A+16B=8 \end{array}$

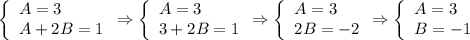
$\left\{\begin{array}{l} A=3 \\ A+2B=1 \end{array} \Rightarrow \left\{\begin{array}{l} A=3 \\ 3+2B=1 \end{array} \Rightarrow \left\{\begin{array}{l} A=3 \\ 2B=-2 \end{array} \Rightarrow \left\{\begin{array}{l} A=3 \\ B=-1 \end{array}$

Тогда частное решение имеет вид:

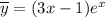
$\overline{y}=(3x-1)e^x$

Общее решение заданного уравнения:

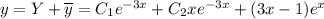
$y=Y+\overline{y}=C_1e^{-3x}+C_2xe^{-3x}+(3x-1)e^x$

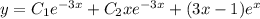
ответ: $y=C_1e^{-3x}+C_2xe^{-3x}+(3x-1)e^x$

4,8(6 оценок)

Ответ:

Supermopsmeni

18.04.2020

Рядом с каждым лжецом должен быть хоть один рыцарь, а рыцарей друг с другом рядом быть не может. Четырёх рыцарей можно легко расставить в квадрате так, чтобы остальное заполнилось лжецами (например, поставив рыцарей по углам). Тогда лжецов будет 4x4 - 4 = 12. Мы привели пример, что такое количество лжецов может быть. Докажем, что это ответ, то есть что больше нельзя. Лжецов можно было бы сделать больше только за счёт уменьшения количества рыцарей. Разобьём квадрат 4x4 на 4 квадратика 2x2. Докажем, что в любом из них должен обязательно быть рыцарь. Действительно, в противном случае весь квадратик 2x2 заполнен лжецами, а лжец, находящийся в углу большого квадрата, не будет соседствовать ни с каким рыцарем, что невозможно. Поскольку квадратиков 2x2 4 штуки, то и рыцарей меньше 4 быть никак не может.

4,7(79 оценок)

Это интересно:

Хобби-и-рукоделие

31.03.2023

Чистка масляных картины: все, что нужно знать, чтобы сохранить ее надолго...

Искусство-и-развлечения

30.04.2020

Как стать сопрано, если вы альт (для девушек)...

03.03.2023

Как пригласить девочку на свидание в пятом классе...

Взаимоотношения

17.05.2021