Пошаговое объяснение:
Задание №1
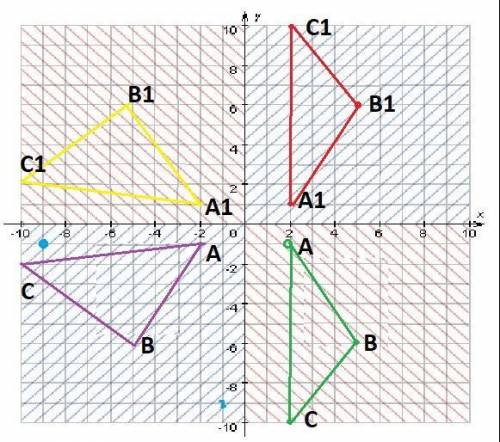
Отметьте точки А (2;1), В(5;6),С(10;2) в системе координат. (КРАСНЫЙ)
Соедините эти точки отрезками и получите треугольник АВС.
Постройте треугольник А1В1С1. симметричный треугольнику АВС, относительно оси абсцисс.
Запишите координаты точек А1, В1, С1.
А1, (2; 1 ) , В1,( 5; -6) С1.( 2 ; -10) зеленый
Задание №2. Треугольник задан координатами своих вершин.
Отметьте точки А (-2;-1), В(-5;-6),С(-10;-2) в системе координат. (СИНИЙ)
Соедините эти точки отрезками и получите треугольник АВС.
Постройте треугольник А1В1С1. симметричный треугольнику АВС, относительно оси ординат..
Запишите координаты точек А1, В1, С1.
А1, (2; 1 ) , В1,( -5; 6) С1.( -10 ; 2) синий
Пошаговое объяснение:
97.
б) x÷(-3)+3≥-6; x÷(-3)≥-6-3; x≤-9·(-3); x≤27; x∈(-∞; 27]
.>x
27
д) x÷(-2)+8<-1; x÷(-2)<-1-8; x>-9·(-2); x>18; x∈(18; +∞)
°>x
18
з) x÷(-4)+4≤-4; x÷(-4)≤-4-4; x≥-8·(-4); x≥32; x∈[32; +∞)
.>x
32
99.
б) x/(-2) -1<2; x/(-2)<2+1; x>3·(-2); x>-6; x∈(-6; +∞)
д) y/(-8) +3≥-2; y/(-8)≥-2-3; y≤-5·(-8); y≤40; y∈(-∞; 40]
з) z/(-7) +3<7; z/(-7)<7-3; z>4·(-7); z>-28; z∈(-28; +∞)
Основная теорема арифметики. Всякое натуральное число п > 1 либо просто, либо может быть представлено, и притом единственным образом - с точностью до порядка следования сомножителей, в виде произведения простых чисел (можно считать, что любое натуральное число, большее 1, можно представить в виде произведения простых чисел, если считать , что это произведение может содержать всего лишь один множитель).
Среди простых сомножителей, присутствующих в разложении `n = p1*p2*...*pk`, могут быть и одинаковые. Например, `24=2*2*2*3`. Их можно объединить, воспользовавшись операцией возведения в степень. Кроме того, простые сомножители можно упорядочить по величине. В результате получается разложение
`n = p_1^(alpha_1)*p_2^(alpha_2)**p_k^(alpha_k)`, где `alpha_1, alpha_2, , alpha_k in NN`
(1)
Такое представление числа называется каноническим разложением его на простые сомножители. Например, каноническое представление числа 2 520 имеет вид 2 520 = 23 • З2 • 5 • 7.
Из канонического разложения числа легко можно вывести следующую лемму: Если n имеет вид (1), то , то все делители этого числа имеют вид:
`d = p_1^(beta_1)*p_2^(beta_2)**p_k^(beta^k)`, где `0 <= beta_m <= alpha_m` ( `m = 1,2,..., k`)
(2)
В самом деле, очевидно, что всякое d вида (2) делит а. Обратно, пусть d делит а, тогда a=cd, где с — некоторое натуральное число и, следовательно, все простые делители числа d входят в каноническое разложение числа а с показателями, не превышающими соответствующих показателей числа а.
Рассмотрим две функции, заданные на множестве натуральных чисел:
а) τ(n) - число всех натуральных делителей n;
2) σ(n) сумма всех натуральных делителей числа n.
Пусть n имеет каноническое разложение (1). Выведем формулы для числа и суммы его его натуральных делителей.
Теорема 1. Число натуральных делителей числа n
`tau(n) = (alpha_1 + 1)*(alpha_2 + 1)**(alpha_k + 1);`
(3)
Доказательство.
читать дальше
Пример. Число 2 520 = 23 • З2 • 5 • 7. имеет (3+1)(2+1)(1+1)(1+1) = 48 делителей.
Теорема 2. Пусть n имеет каноническое разложение (1). Тогда сумма натуральных делителей числа n равна
`sigma(n) = (1 + p_1 + p_1^2 + + p_1^(alpha_1))*(1 + p_2 + p_2^2 + + p_2^(alpha_2))* * (1 + p_k + p_k^2 + + p_k^(alpha_k));`
(4)
Доказательство.
читать дальше
Пример. Найти сумму всех делителей числа 90.
90=2 • З2 • 5. Тогда σ(90)=[(22-1)/(2-1)]• [З3-1)/(3-1)]• [(52-1)/(5-1)]=234
Формула (4) может найти все делители числа.Так, например, чтобы найти все делители числа 90, раскроем скобки в следующем произведении (не производя операцию сложения): (1+2)(1+3+З2)(1+5)=(1+1*3+1*З2+1*2+2*3+2*З2)(1+5) = 1+3+З2+2+2*3+2*З2+ 5+3*5+З2*5+2*5+2*3*5+2*З2*5 = 1+3+9+2+6+18+5+15+45+10+30+90 - слагаемыми являются делители числа 90.
Решим несколько задач на тему "Число и сумма натуральных делителей натурального числа"
Задание 1. Найдите натуральное число, зная, что оно имеет только два простых делителя, что число всех делителей равно 6, а сумма всех делителей — 28.
Решение
Задания из сборника TTZ - ЕГЭ 2010. Математика. Типовые тестовые задания
Задание 2. TTZ.С6.2 Найдите все натуральные числа, которые делятся на 42 и имеют ровно 42 различных натуральных делителя (включая единицу и само число).
Решение
Задание 3. TTZ.С6.9 Найдите все натуральные числа, последняя десятичная цифра которых 0 и которые имеют ровно 15 различных натуральных делителей(включая единицу и само число).
Решение
Задание 4. SPI.С6.9. У натурального числа n ровно 6 делителей. Сумма этих делителей равна 3500. Найти n.
Решение VEk:
Решение
Задания для самостоятельной работы
SR1. Найти все числа, имеющие ровно 2 простых делителя, всего 8 делителей, сумма которых равна 60.
SR2. Найти натуральные числа, которые делятся на 3 и на 4 и имеют ровно 21 натуральный делитель.
SR3. Найти наименьшее натуральное число, имеющее ровно 18 натуральных делителей.
SR4. Найти наименьшее число, кратное 5, имеющее 18 натуральных делителей.
SR5. Некоторое натуральное число имеет два простых делителя. Его квадрат имеет всего 15 делителей. Сколько делителей имеет куб этого числа?
SR6. Некоторое натуральное число имеет два простых делителя. Его квадрат имеет всего 81 делитель. Сколько делителей имеет куб этого числа?
SR7. Найти число вида m = 2x3y5z, зная, что половина его имеет на 30 делителей меньше, треть —на 35 и пятая часть — на 42 делителя меньше, чем само число.