Запишем формулу: P=m/n, где m – число исходов, благоприятствующих осуществлению события X, а n – число всех равновозможных элементарных исходов.
Для начала определим вероятность выпадения орла или решки при одном броске. Выпадает всегда 1 результат, а всего исходов 2. Значит, вероятность выпадения орла или решки = 1/2. Но бросков мы делаем 2, а значит, количество исходов возводится в квадрат и теперь равно 1 / 2 × 2 = 1/4. В последующем мы будем домножать числитель на количество удовлетворяющих нас исходов.
Значение "Решка выпала хотя бы 1 раз" верно при следующих результатах:
1) решка и орёл
2) орёл и решка
3) решка и решка
Как видим, количество удовлетворяющих нас результатов =3, а значит, в двух бросках решка выпадает хотя бы один раз с вероятностью 1 × 3 / 4 = 3/4 = 0.75 = 75%
В первый раз выпал орёл при следующих результатах:
1) орёл и решка
2) орёл и орёл
Как видим, количество удовлетворяющих нас результатов =2, а значит, в двух бросках орёл выпадет первым с вероятностью 1 × 2 / 4 = 2/4 = 1/2 = 0.5 = 50%
ответ: 75%, 50%.
1)
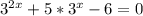
Выполним замену:
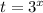
t² + 5t - 6 = 0
D = 5² - 4 * (- 6) = 25 + 24 = 49
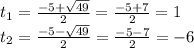
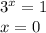
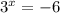 - решений нет.
- решений нет.
ответ: х = 0.
2)
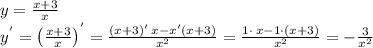
ответ: 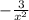 .
.
3)
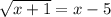
ОДЗ: x ≥ 5
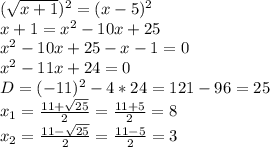
Второй корень не подходит.
ответ: х = 8.
4)
f(x) = 3x² - 2x + 4
F(x) = x³ - x² + 4x + C
5)
Четырёхугольная призма по условию является правильной, значит это прямоугольный параллелепипед, в основании которого лежит квадрат.
Найдём сторону основания:
S(основания) = 144 (см²);
√144 = 12 (см).
Найдём диагональ основания (по т. Пифагора):
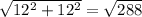 (см)
(см)
Найдём диагональ призмы (по т. Пифагора):
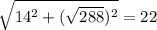 (см)
(см)
ответ: 22 см.
49-22=27 человек в классе (вычитаем учеников которые сдавали сразу 2 экзамена)
ответ 27 человек в классе