1)Записать уравнение плоскости по трём точкам А, В, с, если
А(7; -1; -2), В(1; 7; 8), С(3; 7; 9).
2)Найти уравнение прямой
3)Доказать, что векторы a, b, c образуют базис и записать вектор d в базисе (a, b, c), если a(-1, 2, -3); b(0, 2, 4); c(3, -1, 4) и d(-2, 3, 2).
1) Для составления уравнения плоскости используем формулу:
x - xA y - yA z - zA
xB - xA yB - yA zB - zA
xC - xA yC - yA zC - zA = 0
Подставим данные и упростим выражение:
x – 7 y - (-1) z - (-2)
1 – 7 7 - (-1) 8 - (-2)
3 – 7 7 - (-1) 9 - (-2) = 0
x – 7 y - (-1) z - (-2)
-6 8 10
-4 8 11 = 0
(x – 7 )(8·11-10·8) - (y - (-1))((-6)·11-10·(-4)) + (z - (-2))((-6)·8-8·(-4)) = 0
8(x – 7) + 26(y - (-1)) + (-16)(z - (-2)) = 0
8x + 26y - 16z - 62 = 0
4x + 13y - 8z - 31 = 0.
2) Дана прямая d как линия пересечения плоскостей:
{3x+2y-z-1=0; 2x-y+3z-4=0)
Направляющий вектор “p” нашей прямой ортогонален нормальным векторам n1 и n2 плоскостей. А если , то вектор «p» найдём как векторное произведение векторов нормали: .
Из уравнений плоскостей {(3x+2y-z-1=0; 2x-y+3z-4=0) снимаем их векторы нормали:
n1(3; 2; -1), n2(2; -1; 3).
И находим направляющий вектор p прямой d, перпендикулярный двум заданным с векторного произведения.
I j k| I j
3 2 -1| 3 2
2 -1 3| 2 -1 = 6i - 2j - 3k - 9j - 1i – 4k = 5i - 11j - 7k.
Вектор p = (5; -11; -7).
Можно применить готовую формулу для определения направляющего вектора линии пересечения двух плоскостей.
p ⃗(|(B_1&[email protected]_2&C_2 )||(C_1&[email protected]_2&A_2 )||(A_1&[email protected]_2&B_2 )|)
p = (2*3 – (-1)*(-1); -1*2-3*3; 3*(-1)-2*2) = (5; -11; -7).
Далее надо найти точку на прямой.
Так как линия пересекает плоскость хОу, то в этой точке координата z = 0.
Поэтому в системе уравнений нужно обнулить координату z.
Пусть z = 0, тогда получаем систему двух линейных уравнений с двумя неизвестными: {([email protected]=0) {([email protected]=0)
Почленно складываем уравнения и находим решение системы:
7x - 9 = 0,
x = 9/7,
y = 2х – 4 = 2(9/7) – 4 = -10/7.
Таким образом, точка M((9/7); (-10/7); 0) принадлежит данной прямой.
Выполним проверку: подставим координаты точки M((9/7); (-10/7); 0) в исходную систему уравнений:
{(3(9/7)+2(-10/7)-0-1=27/7-20/7-7/7=0; 2(9/7)-(-10/7)+3*0-4=18/7+10/7-28/7=0)
Получены верные равенства, значит, действительно, M ∈ d.
Тогда по точке M((9/7); (-10/7); 0) и направляющему вектору p=(5; -11; -7) составляем уравнение прямой:
(x-(9/7))/5 = (y + (10/7))/(-11) = z/(-7).
3) Даны векторы a(-1;2;-3), b(0;2;4), c(3;-1;4), d(-2;3;2).
Показать, что векторы образуют базис трехмерного пространства и найти координаты вектора d в этом базисе.
Данная задача состоит из двух частей. Сначала необходимо проверить образуют ли векторы базис. Векторы образуют базис, если определитель, составленный из координат этих векторов, отличен от нуля, в противном случае вектора не являются базисными и вектор d нельзя разложить по данному базису.
Вычислим определитель матрицы:
E = -1 2 -3
0 2 4
3 -1 4
∆ = -1*(2*4 - (-1)*4) - 0*(2*4 - (-1)*(-3)) + 3*(2*4 - 2*(-3)) = 30.
Определитель матрицы равен ∆ =30.
Так как определитель отличен от нуля, то векторы образуют базис, следовательно, вектор X можно разложить по данному базису. Т.е. существуют такие числа α1, α2, α3, что имеет место равенство:
X = α1*a + α2*b + α3*c.
Запишем данное равенство в координатной форме:
(-2;3;2) = α(-1;2;-3) + α(0;2;4) + α(3;-1;4).
Используя свойства векторов, получим следующее равенство:
(-2;3;2) = (-1α1;2α1;-3α1;) + (0α2;2α2;4α2;) + (3α3;-1α3;4α3;)
(-2;3;2) = (-1α1 + 0α2 + 3α3;2α1 + 2α2 -1α3;-3α1 + 4α2 + 4α3)
По свойству равенства векторов имеем:
-1α1 + 0α2 + 3α3 = -2
2α1 + 2α2 -1α3 = 3
-3α1 + 4α2 + 4α3 = 2
Решаем полученную систему уравнений методом Крамера.
Dx1 = -2 0 3
3 2 -1 = 0 x1 = 0
2 4 4
Dx2 = -1 -2 3
2 3 -1 = 35 x2 = 35/30=7/6
-3 2 4
Dx3 = -1 0 -2
2 2 3 = -20 x3 = -20/30=-2/3
-3 4 2
X = 0
7/6
-2/3
X = (7/6)b - (2/3)c.
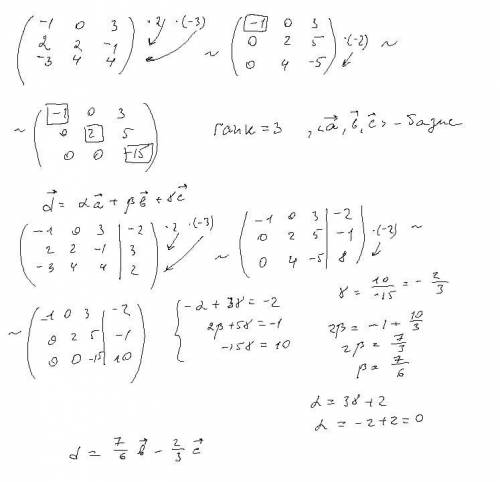
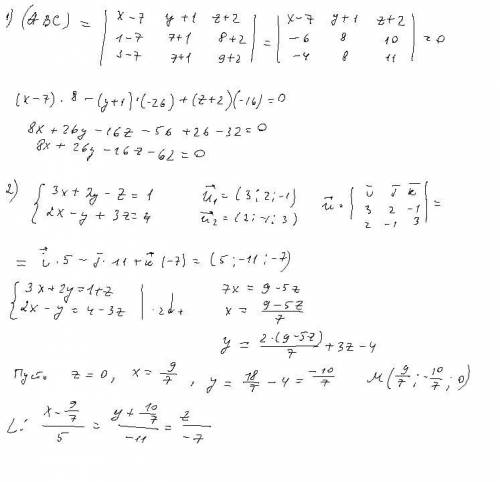
А(-1;0),В(4;0),С(1;-2), найти:
1) уравнение высоты АД.
Высота АД – это перпендикуляр к стороне ВС.
Вектор ВС = (1-4; -2-0) = (-3; -2).
Уравнение прямой ВС: (х – 4)/(-3) = у/(-2) каноническое
-2х + 8 = -3у
2х - 3у – 8 = 0 общее.
Для прямой в общем виде Ax + By + C = 0 перпендикулярная прямая меняет коэффициенты А и В на –В и А (из условия, что их скалярное произведение равно 0).
Тогда уравнение перпендикулярной прямой к прямой ВС будет иметь вид:
3x + 2y + С = 0. Для определения слагаемого С подставим координаты точки А(-1; 0).
3*(-1) + 2*0 + C = 0, отсюда С = 3.
ответ: 3x + 2y + 3 = 0.
2) уравнение прямой, проходящей через А параллельно ВС.
Коэффициенты при переменных у этой прямой такие же, как и у прямой ВС: 2х - 3у + С = 0. Подставим координаты точки А(-1; 0).
2*(-1) – 3*0 + С = 0, отсюда С = 2.
Получаем уравнение 2х - 3у + 2 = 0.
3) уравнение прямой, соединяющей середины сторон АВ и ВС.
Коэффициенты при переменных у этой прямой такие же, как и у прямой АС. Вектор АС = С(1;-2) - А(-1;0) = (2; -2).
Уравнение АС: (х + 1)/2 = у/(-2) или х + у + 1 = 0.
Найдём середину Д стороны АВ.
Д = (А(-1;0)+В(4;0))/2 = (1,5; 0).
Подставим координаты точки Д в уравнение прямой х + у + С = 0.
1,5 + 0 + С = 0, отсюда С = -1,5.
Уравнение х + у - 1,5 = 0 или в целых числах 2х + 2у - 3 = 0.
4) угол А треугольника АВС. А(-1;0),В(4;0),С(1;-2).
Находим векторы и их модули.
АВ = (4-(-1); 0-0) = (5; 0). |AB| = 5.
AC = (2; -2). |AC) = √(2² + (-2)²) = √(4 + 4) = √8 = 2√2.
Теперь находим косинус угла А.
cos A = (5*2 + 0*(-2))/(5*2√2) = 10/(10√2) = 1/√2.
Угол А = arccos(1/√2) = 45 градусов.
Чтобы перебрать их все, нужно 4000 секунд.
1) Если известна третья цифра а, то остается перебрать 100 вариантов,
от 00а до 99а. Всего 400 сек.
2) Если известна одна цифра, но неизвестно место, то это варианты
от а00а до а99, от 0а0 до 9а9 и от 00а до 99а. Всего 300 вариантов.
Но, если мы перебрали варианты от а00 до а99 и ничего не подошло,
то в вариантах от 0а0 до 9а9 можно пропустить первую цифру а.
Остается 9*10 = 90 вариантов. А если и эти не подошли, то в вариантах от 00а до 99а можно пропустить и 1-ую и 2-ую цифры а. Остается 81.
Всего 100 + 90 + 81 = 271 вариант, и на это нужно 271*4 = 1084 сек.
3) Сумма трех чисел кода нечетна в половине случаев, поэтому нужно 4000/2 = 2000 сек, чтобы перебрать их все.
ответ: 1) 100, 2) 1084, 3) 2000