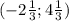f'(x)=d/dx((2+4)⁴*(2-3)³)=f'(x)=d/dx(6⁴*(2-3)³)=f'(x)=d/dx(6⁴*(-1)³)=f'(x)=d/dx(6⁴*(-1))=f'(x)=d/dx(-6⁴*1)=f'(x)=d/dx(-6⁴)=f'(x)=0
Пошаговое объяснение:
Возьмём производную от обеих частей:
f'(x)=d/dx((2+4)⁴*(2-3)³)
Сложим числа 2+4:
f'(x)=d/dx(6⁴*(2-3)³)
Вычислим разность чисел 2-3:
f'(x)=d/dx(6⁴*(-1)³)
Вычислим степень (-1)³:
f'(x)=d/dx(6⁴*(-1))
Произведение положительного и отрицательного значений отрицательно:(+)*(-)=(-):
f'(x)=d/dx(-6⁴*1)
Любое выражение умножение на 1,не изменяется:
f'(x)=d/dx(-6⁴)
Производная констакты d/dx(-6⁴) всегда равна 0:
f'(x)=0
1) 4 < а < 5 |*(-2) 2 < b < 7 |*6
-2*4 > -2a > -2*5 6*2 < 6b < 6*7
-8 > -2a > -10 12 < 6b < 42
-10 < -2a < -8
12 < 6b < 42
10 < -2a < -8 +
12+10 < 6b-2a < 42-8
22 < 6b-2a < 34
Итак, 6b-2a находится в промежутке (22;34)
2) 4 < а < 5 :
2 < b < 7
4/2 > a/b > 5/7
2 > a/b > 5/7
5/7 < a/b < 2
Итак, a/b находится в промежутке (5/7; 2)
3) 2 < b < 7 |*4/3
(4/3)*2 < 4/3*b < (4/3)*7
8/3 < 4/3 *b < 28/3 |-5
8/3 -5 < 4/3*b-5 < 28/3 -5
8/3 - 15/3 < 4/3*b < 28/3-15/3
-7/3 < 4/3*b < 13/3
-2 1/3 < 4/3*b < 4 1/3
Итак, 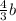 находится в промежутке
находится в промежутке