тригонометрический круг — это самый простой способ начать осваивать тригонометрию. он легко запоминается, и на нём есть всё необходимое.тригонометрический круг заменяет десяток таблиц.
вот что мы видим на этом рисунке: перевод градусов в радианы и наоборот. полный круг содержит градусов, или радиан.значения синусов и косинусов основных углов. помним, что значение косинуса угла мы находим на оси , а значение синуса — на оси .и синус, и косинус принимают значения от до .значение тангенса угла тоже легко найти — поделив на . а чтобы найти котангенс — наоборот, косинус делим на синус.знаки синуса, косинуса, тангенса и котангенса.синус — функция нечётная, косинус — чётная.тригонометрический круг увидеть, что синус и косинус — функции периодические. период равен.
20
Пошаговое объяснение:
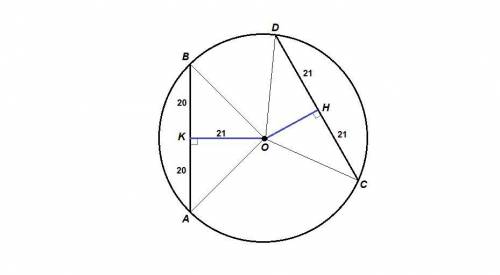
Соединим центр окружности с концами хорд.
ОА = ОВ = ОС = OD как радиусы.
Проведем ОК⊥АВ и и OH⊥CD,
ОК = 21 - расстояние от центра до АВ,
ОН - искомое расстояние от центра до CD.
ΔОАВ равнобедренный, значит ОК - высота и медиана. ⇒
АК = КВ = 1/2АВ = 1/2 · 40 = 20
Из прямоугольного треугольника АКО по теореме Пифагора:
АО = √(АК² + КО²) = √(20² + 21²) = √(400 + 441) = √841 = 29
СО = АО = 29
ΔCOD равнобедренный, значит OН - высота и медиана, ⇒
СН = HD = 1/2CD = 1/2 · 42 = 21
Из прямоугольного треугольника СОН по теореме Пифагора:
OH = √(CO² - CH²) = √(29² - 21²) = √(841 - 441) = √400 = 20
Основная задача рекреалогии - изучение содержания и условий деятельности человека, осуществляемой в нерабочее время.