Пошаговое объяснение:
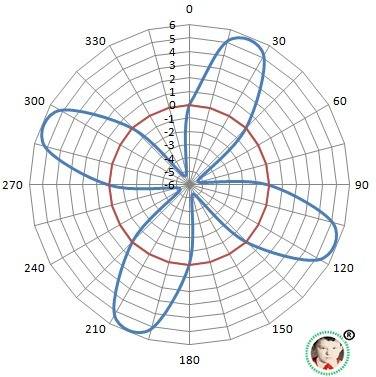
Варианты такого графика в полярных координатах на рисунках в приложении. Изменение частоты приводит к появлению "лопастей".
Самое нужное - на последнем рисунке с расчётной таблицей.
Обратить внимание, что окружность с радиусом 0 - не в центре полярной системы координат. На графике есть точки R=+6 - с наружи и с R=-6 - в центре системы координат.
С физической точки зрения отрицательных расстояний не может быть и, поэтому, задача чисто математическая - красивые фигуры и никакой пользы.
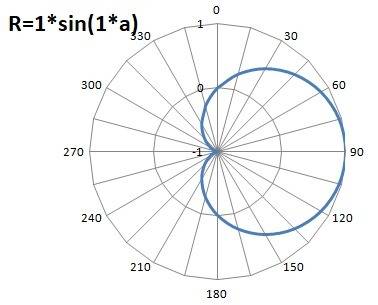
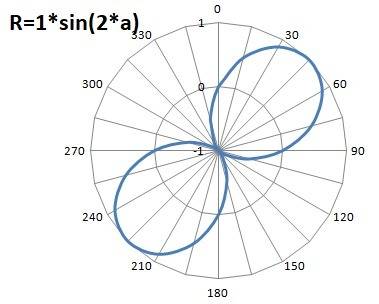
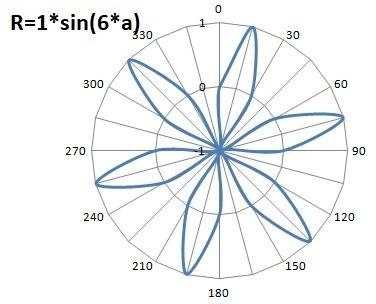
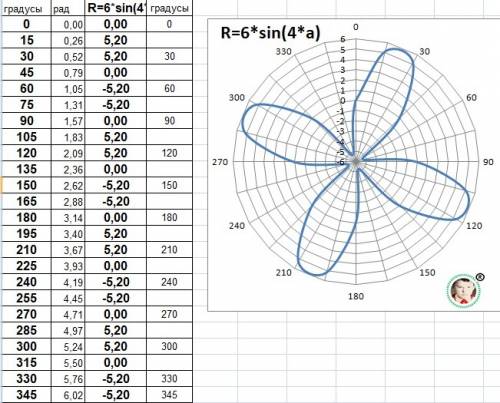
Пошаговое объяснение:
Направление движения: на встречу друг другу.
Выехали из двух пунктов одновременно.
Расстояние между пунктами А и В 300 км.
Время движения 1,5 ч.
Скорость второго автомобиля на 6 км/ч меньше скорости второго автомобиля.
Определить скорость каждого автомобиля.
Расстояние, на которое сближаются два автомобиля за единицу времени, называют скоростью сближения vсбл.
В случае движения двух объектов навстречу друг другу скорость сближения равна: vсбл = v1 + v2.
Если начальная расстояние между пунктами А и В равна S километров и два автомобиля встретились через tвстр ч, то S = vсбл * tвстр = (v1 + v2) * tвстр, км.
Пусть скорость второго автомобиля v1 примем за х км/ч, тогда скорость v2 первого автомобиля равна (х + 6) км/ч.
Согласно условию задачи, нам известно, что расстояние между пунктами А и В равно S = 300 км и tвстр = 1,5 ч, подставим значения в формулу:
(х + (х + 6)) * 1,5 = 300
(х + х + 6) * 1,5 = 300
(2х + 6) * 1,5 = 300
3х + 9 = 300
3х = 300 - 9
3х = 291
х = 291 : 3
х = 97
Скорость второго автомобиля равна 97 км/ч.
Скорость первого равна: 97 + 6 = 103 км/ч.
ответ: скорость первого автомобиля — 103 км/ч; скорость второго автомобиля — 97 км/ч.
2. 2400:60 = 40 км/ч — скорость мотоциклиста.
3. 960:40 = 24 часа — в 1 неделю.
4. 1440:40 = 36 часов — во 2 неделю