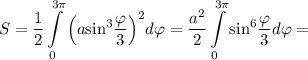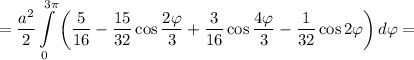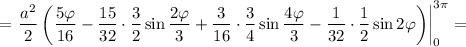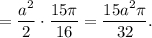Объяснение:
Дано: пусть ∆АВС, АВ = ВС = 8см, АС = 12см
Найти: DO - ?
⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀⠀Решение Это ромб. Стороны попарно параллельны и диагонали перпендикулярны и точкой пересечения делятся пополам. DО=ОВ. AO=OC=6см∆АВО - прямоугольный. Найдем Катет (ВО) применив теорему Пифагора. Она гласит, что квадрат гипотенузы равен сумме квадратов катетов.⠀⠀⠀⠀AB²=BO² + AO²
⠀⠀⠀⠀8² = ВО² + 6²
Отсюда выразим катет ВО.⠀⠀⠀⠀ВО² = 8² - 6²
⠀⠀⠀⠀ВО² = 64 - 36
⠀⠀⠀⠀ВО² = 28
Извлечем корень.⠀⠀⠀⠀ВО = √28
⠀⠀⠀⠀ВО = 2√7(см)
Т.к. ВО = DO, то ответ 2√7(см)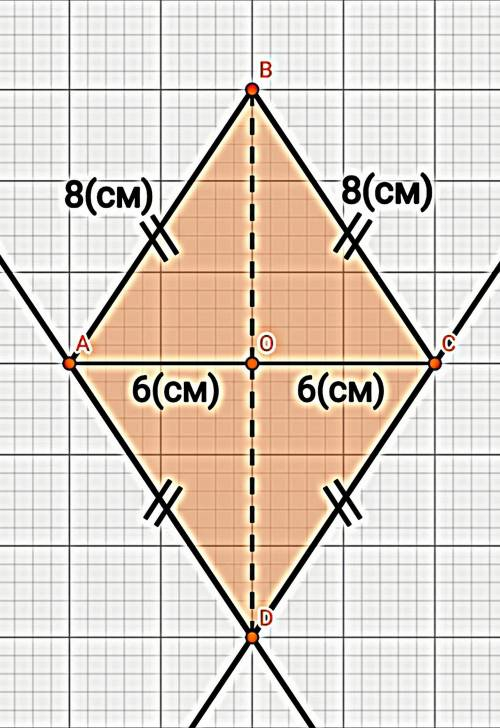
а) 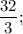 б) 2; в)
б) 2; в) 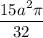
Пошаговое объяснение:
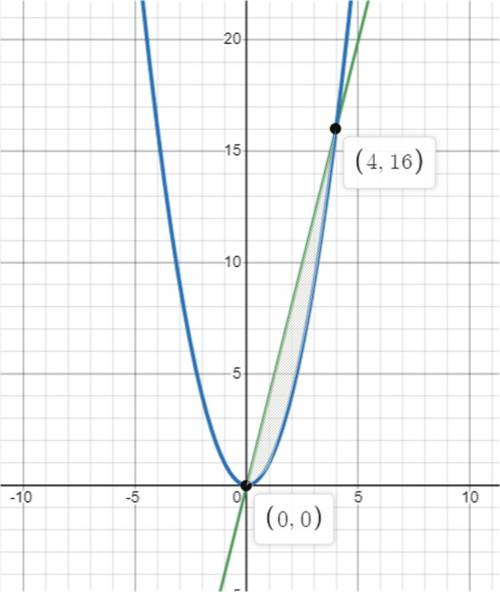
а) Найдем точки пересечения указанных графиков 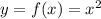 и
и 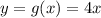 (рис. 1), приравняв правые части:
(рис. 1), приравняв правые части:
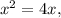
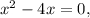
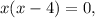
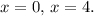
Так как на промежутке ![[0;\,\,4]](/tpl/images/4978/6389/04e4e.png)
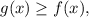 то применяя формулу Ньютона-Лейбница, получаем
то применяя формулу Ньютона-Лейбница, получаем
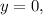
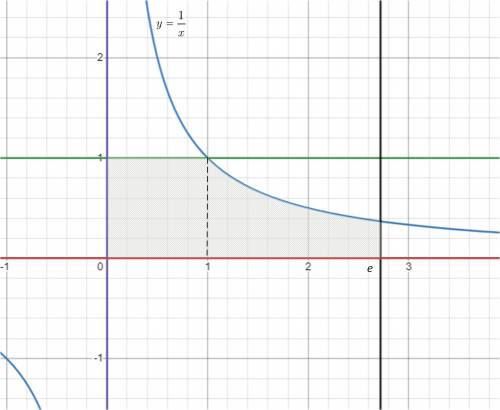
б) Нарисуем в одной координатной плоскости все указанные линии и заштрихуем область, площадь которой необходимо найти. Разобьем получившуюся фигуру на две части прямой 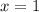 (рис. 2).
(рис. 2).
Тогда левая часть фигуры — квадрат со стороной 1, его площадь равна 1.
Площадь правой части фигуры найдем как площадь криволинейной трапеции, ограниченной графиком функции 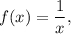 прямыми
прямыми 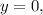
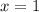 и
и 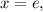 используя формулу Ньютона-Лейбница:
используя формулу Ньютона-Лейбница:
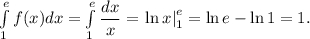
Таким образом, площадь заданной фигуры равна 1 + 1 = 2.
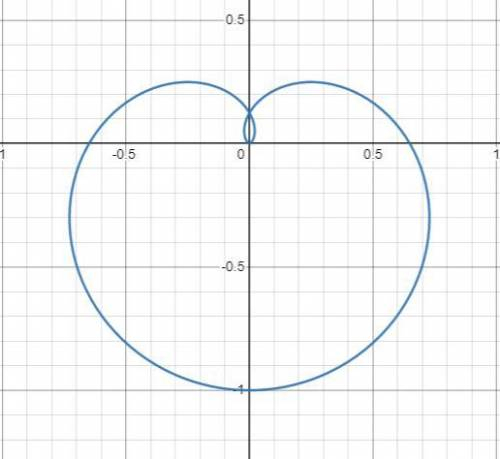
в)
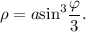
(рис. 3 для случая 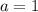 ).
).
Решаем неравенство
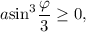
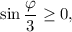
![\displaystyle\frac{\varphi }{3} \in [\pi k;\,\,\pi + \pi k],\\](/tpl/images/4978/6389/95d76.png)
![\varphi \in [3\pi k;\,\,3\pi + 3\pi k].](/tpl/images/4978/6389/60642.png)
Для вычисления площади криволинейного сектора воспользуемся формулой
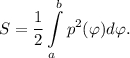
Из формулы синуса тройного угла следует, что
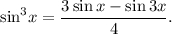
Тогда
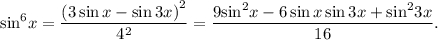
Понижая степень синуса и записывая произведение синусов в виде суммы, получим
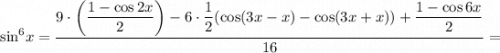
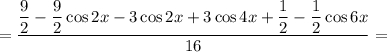
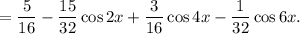
Тогда площадь