Оператор должен набрать 0,5 всех страниц. рукописи. когда он набрал 0,7 рукописи ему осталось набрать. ещё. 6 страниц . сколько всего страниц в рукописи ? волк стал догонять лису, когда между ними было. 75 3/5. м. скорость волка 16,8 м /с . лиса убегала от волка со скоростью 10,5 м /с . через сколько секунд волк догонит лису ?
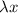 , вместо у подставляем
, вместо у подставляем 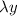 , производную не трогаем.
, производную не трогаем.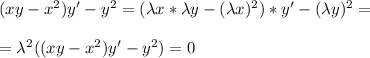
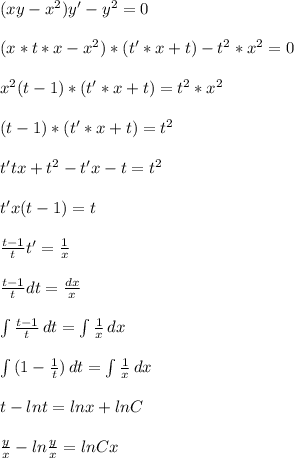
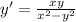
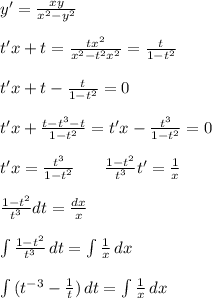
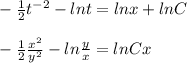
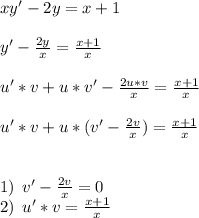
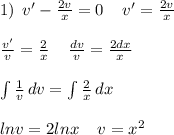
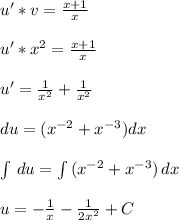
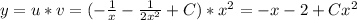
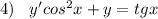
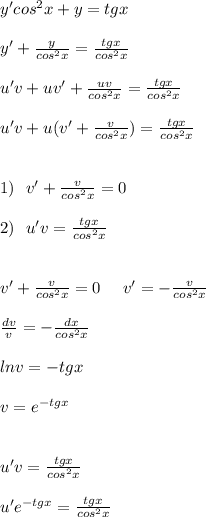
![u' = e^{tgx} * \frac{tgx}{cos^2x} \\ \\ u = \int\limits {e^{tgx}*\frac{tgx}{cos^2x}} \, dx \:\:\:\:\:\: [t=tgx; \:\:\:\:\:\: dt = \frac{dx}{cos^2x}] \\ \\ u = \int\limits {e^{t}* t} \, dt = e^t *t - \int\limits {e^t} \, dt = e^t*t - e^t = e^t*(t-1) +C = \\ \\ \\ f = t; \:\:\:\:\:\: df = dt; \:\:\:\:\:\: dg = e^t dt; \:\:\:\:\:\: g = e^t \\ \\ \\ = e^{tgx}(tgx-1) + C](/tpl/images/0889/8799/c82d0.png)
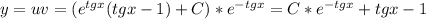
2)Найдем сколько страниц должен набрать оператор.Правило:чтобы найти число по велечине данной его части,надо эту величину разделить на дробь,выражающую данную часть,тогда 6/0,3=20 страниц,что соответствует 0,5 всех страниц рукописи
3)Найдем сколько всего странци в рукописи,воспользовавшись вышеуказанным правилом,20/0,5=40 страниц
ответ 40 страниц
СЛЕДУЮЩАЯ ЗАДАЧА
Примем
Скорость волка-А=16(4/5)=16,8 м/с
Скорость лисы-В=10(1/2)=10,5 м/с
Первоначальное расстояние между волком и лисой каждую секунду скоращалось на 6,3 метра
С/(А-В)=75,6/6,3=12с
ответ:через 12 секунд волк догонит лису