7
Пошаговое объяснение:
Вспомним признак делимости на 9: число делится на 9 тогда и только тогда, когда его сумма цифр делится на 9.
Этот признак работает и для равноостаточности при делении на 9. То есть, число и его сумма цифр имеют одинаковый остаток при делении на 9.
Пусть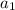 
- изначальное число и 
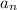- сумма цифр числа 
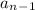. Пусть остаток при делении на 9 у числа 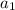- r, тогда и у числа 
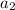остаток при делении на 9 тоже r. Но тогда и у чисел 
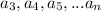остаток при делении на 9 равен r. Но так как r - чисто от 0 до 9, то это и есть наша оставшаяся в конце цифра.
Тогда нам нужно всего лишь найти остаток при делении на 9 у числа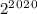 
. А он такой же, как у числа 
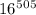, и такой же, как у числа 
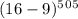, и такой же, как у числа 
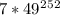, а он такой же, как у числа 
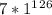, а это равно 7.
x = -2.
ODZ: x belongs to [-2; 2].
Пошаговое объяснение:
In order to find the domain of definition of the function y = √ (4 - x ^ 2) (quadruple root), we start by considering it.
So, we are given a function whose variable is under the sign of the quadruple root.
In order for the function to have a value, the radical expression must be non-negative.
We need to find a solution to the following inequality:
4 - x ^ 2 ≥ 0;
We apply the formula difference of squares to the left side of the inequality:
(2 - x) (2 + x) ≥ 0;
Looking for points:
2 - x = 0;
x = 2;
2 + x = 0;
x = -2.
ODZ: x belongs to [-2; 2].
66,85