Площа повної поверхні прямої призми:
Sп=2Soc+Sb.
В основі прямої призми лежить рівнобічна трапеція з основами AD=4 см і BC=10 см і бічною стороною AB=CD=5 см.
трапеція
Знайдемо висоту DL трапеції.
Із прямокутного трикутника DLC (∠DLC=90, бо DL⊥BC, CD=5 см – гіпотенуза і CL=3 см – катет) знайдемо катет DL.
DL2=CD2-CL2, звідси
Площа основи – трапеції ABCD:
Периметр основи:
Poc=AB+BC+CD=2•5+10+4=24 см.
Площа бічної поверхні:
Sб=Poc•h=24•10=240 см2.
Площа повної поверхні прямої призми:
Sп=2Soc+Sb=2•28+240=296 см2.
Відповідь: 296 см2
Пошаговое объяснение:
100 человек
Пошаговое объяснение:
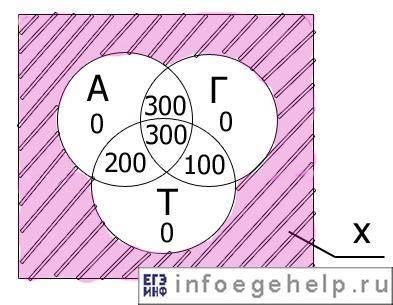
Число тех, кто не решил ни одной задачи возьмём за х
800 задач решили по алгебре
700 задач решили по геометрии
600 задач решили по тригонометрии
А+Г=600 школьников
А+Т=500 школьников
Г+Т=400 школьников
А+Г+Т= 300 школьников
1) А+Г+Т=800+700+600=2100 -всего решили задач по А,Г,Т
т.к. 300 человек (которые решили по три задачи) учтены при А+Г, А+Т, Г+Т определим сколько человек решили по две задачи.
2) А+Г=600 - 300=300 чел решили только две задачи А+Г
3) А+Т=500- 300 =200 чел решили только две задачи А+Т
4) Г+Т=400-300= 100 чел. решили только две задачи Г+Т
5) 300+200+100=600 человек решили две задачи
6) 600*2+300*3=1200+900=2100 задач решили школьники (которые решили по две и по три задачи)
7)2100-2100=0- задач решили школьники (которые решили только по одной задачи)
8) 300+600=900 школьников решили две и более задач
9) 1000-900=100 школьников ничего не решили
ответ: 100 школьников ничего не решили.
Ниже прикрепил картинку, чтобы было видно визуально
а) 81а² - (9а - 7b)*2 = 81a² - 2*9a + 2*7b = 81а² -18а +14b
если в условии опечатка (^2) :
81a² - (9a -7b)² = 81a² - (81a² - 2*9a*7b + 49b²) =
= 81a² -81a² +126ab - 49b² = 126ab - 49b² =
можно еще вынести общий множитель:
= 7b*(18a -7b)
б) (8x-y)²-64x² = 64x² - 16xy +y² - 64x² = y² - 16xy =
общий множитель:
= y(y -16x)
в) 2 *(а-b² ) = 2a - 2b²
если в условии опечатка:
2*(а-b)² = 2 * (a² -2ab +b²) = 2a² -4ab +2b²
г) х(7-х) -(4-х) =7х - х² - 4 + х = -х² +8х - 4
№2.
а) а²+6ab +9b² = a² +2*a*3b + (3b)² = (a+3b)²
б)-25x² + 10xy -y² = - (25x² - 10xy +y²) = -((5x)² - 2*5x*y +y²) = - (5x -y)²
в)12х +х² + 36 = х² + 2*х * 6 + 6² = (х+6)²
№3.
х + (5х+2)² = 25 *(1+х²)
х + 25х² + 2*5х *2 + 2² = 25 + 25х²
х + 25х² + 20х + 4 = 25 + 25х²
21х + 25х² - 25х² = 25-4
21х=21
х=21:21
х=1
проверим:
1 +(5*1+2)² = 25 * (1 + 1²)
1 + 7² = 25 * (1+1)
1 + 49 = 25*2
50 = 50