войти
января 21: 11
в первый день тракторная бригада вспахала 3/8 участка , во второй день - 2/5 остатка, а в третий день - остальные 216га.определите
площадь участка.
ответ или решение1
горшков мстислав
1) примем за 1 (единицу) площадь всего участка и узнаем, какую часть составляет участок, который остался после первого дня работы: 1 – 3/8 = 5/8;
2) вычислим, какую часть участка составляет площадь, вспаханная во второй день: 5/8 · 2/5 = 1/4;
3) определим, какую часть площади вспахали в третий день: 5/8 – 1/4 = 3/8;
4) зная, что 3/8 часть от всей площади участка – это 216 га, узнаем, чему равна площадь этого участка: 216 : 3/8 = 216 · 8 : 3 = 576 (га).
ответ: площадь участка – 576 га.
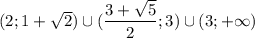
Пошаговое объяснение:
ОДЗ логарифмов: x > 0, x ≠ 1, x > 2, x ≠ 3 ⇒ x > 2, x ≠ 3
Пусть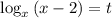 
. Тогда 
:
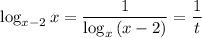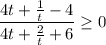. Заметим, что t ≠ 0, так как это значение достигается только при x = 3 (x - 2 = x⁰ = 1 ⇔ x = 3). Но при x = 3 основание логарифма 
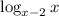равно 1, что не удовлетворяет ОДЗ. Значит, домножим обе части дроби на t:
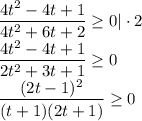
Решим методом интервалов:
+ - + +
----o----o----*---->
-1 -¹/₂ ¹/₂
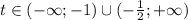
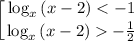
Заметим, что по ОДЗ x > 2, то есть основание логарифма всегда больше 1. Значит, на ОДЗ неравенства равносильны:
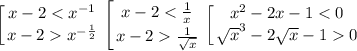
Первое неравенство имеет решение (с учётом ОДЗ)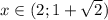 
Второе неравенство раскладывается на множители:
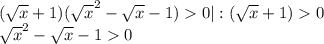
Нули получившегося неравенства: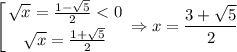 
C учётом ОДЗ получаем, что в данном случае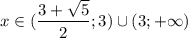 
(левая граница меньше правой, так как √5 < 3).
Объединим промежутки. Сравним правую границу первого неравенства и левую границу второго. Сравним эти числа относительно 2,5:
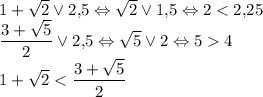
Тогда промежутки не пересекаются, итоговый ответ: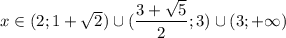 
396 = 3x + x + 156
4x+156=396
4x=396-156
4x=240
x=60
Итак, второе число = 60
1 число = 60*3=180
Проверка: 180+60+156= 396
396=396
ответ: 60 и 180