расстояние между двумя по реке 80 км. пароход совершает этот путь в два конца за 8ч 20мин. определить скорость парохода в стоячей воде, считая скорость течения реки 4 км/ч.
пусть х собственная скорость парохода, тогда на путь по течению он затратит 80/(х+4) часа, против течения 80/(х-4) часа. пароход совершает этот путь в два конца за 8ч 20мин=8⅓часа
80/(х+4)+ 80/(х-4)= 8⅓
80(х-4)+80(х+4)= 8⅓*(х-4)(х+4)
160х=25/3(х²-16)
480х=25х²-400
25х²-480х-400=0
5х²-96х-80=0
д=(-96)²-4*5*(-80)=9216+1600=10816
х₁=96+√10816/2*5=96+104/10=200/10=20
х₂=96-√10816/2*5=96-104/10=-8/10=-0,8 ( скорость отрицательной быть не может)
ответ: скорость парохода в стоячей воде или собственная скорость парохода равна 20км/час
удачи!
1)
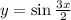 ; Синус - это периодическая функция.
; Синус - это периодическая функция.
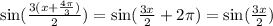 ; Поэтому у данной функции есть период. Просмотрим остальные:
; Поэтому у данной функции есть период. Просмотрим остальные:
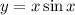 ; Пусть у этой функции есть период T:
; Пусть у этой функции есть период T: 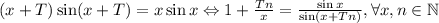 ; Выберем такое число x и n, что выполняются следующие условия:
; Выберем такое число x и n, что выполняются следующие условия: 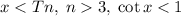 ; Тогда левая часть будет больше правой, что невозможно.
; Тогда левая часть будет больше правой, что невозможно.
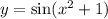 ; Пусть функция имеет период T:
; Пусть функция имеет период T:
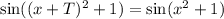
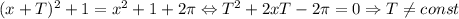 ; Получили противоречие.
; Получили противоречие.
С оставшимися аналогично.
ответ: А;
2) 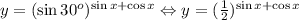 ; Функция монотонно убывает по мере роста показателя степени.
; Функция монотонно убывает по мере роста показателя степени.
Заметим, что 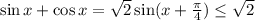 ; Значит,
; Значит,  ;
;
3) 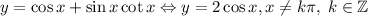 ; С этими условиями область значений равна [-2;2]; Если брать в расчет все значения x, то придется выколоть все точки с ординатами 2 или -2; Получаем, что E(f)=(-2;2);
; С этими условиями область значений равна [-2;2]; Если брать в расчет все значения x, то придется выколоть все точки с ординатами 2 или -2; Получаем, что E(f)=(-2;2);
4) Пусть sin A - первый корень какого-нибудь квадратного трехчлена, а -cos A - его второй корень. Тогда квадратное уравнение примет такой один из возможных видов: 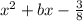 ;
;
В итоге, получаем: 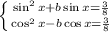 ; Сложим два уравнения:
; Сложим два уравнения:
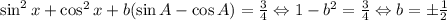 ;
;
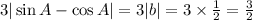
рассмотрим остаток от деления на 1001 нескольких чисел состоящих из семерок, начнем с числа 7777
7777 : 1001 = 7(ост.77),
далее число 77777
77777 : 1001 = 77(ост.70)
далее число 777777
777777 : 1001 = 777(ост. 0)
смотртм, сколько в числе 777777 цифр, в числе 777777 шесть цифр, попробуем разделить 300 : 6 = 50, значит число, состоящее из 300 семерок, можно разбить на 50 чисел, являющихся 777777, значит, остаток от деления числа, состоящего из 300 семерок на 1001, равно 0
ответ: остаток равен 0