10.5. Свойства производных, связанные с арифметическими действиями над функциями
Теорема 3. Если функции y1 = f1(x) и y2 = f2(x) заданы в окрестности точки x0 принадлежит R, а в самой точке x0 имеют конечные производные, то функции lamda1 f1(x) +lamda2 f2(x), lamda1 принадлежит R, lamda1 принадлежит R, f1(x)f2(x), а в случае f2(x0)не равно0 и функции f1(x)/f2(x) также имеют в точке x0 конечные производные; при этом имеют место формулы
(lamda1 y1 +lamda2 y2)' = lamda1 y'1 +lamda2 y'2, (10.21)
(y1y2)' = y'1y2 + y1y'2, (10.22)
(10.23)
(в формулах (10.21)-(10.23) значения всех функций взяты при x = x0).
Прежде всего заметим, что в силу условий теоремы в точке x0 существуют конечные пределы
(дельтаy1/дельтаx) = y'1, (дельтаy2/дельтаx) = y'2.
Докажем теперь последовательно формулы (10.21)-(10.23).
1) Пусть y = lamda1 y1 +lamda2 y2; тогда
дельта y = (lamda1( y1 + дельтаy1) + lamda2( y2 + дельтаy2)) - (lamda1y1 + lamda2y2) = lamda1дельтаy1 + lamda2дельтаy2
и, следовательно,
дельтаy1/дельтаx = lamda1дельтаy1/дельтаx + lamda2дельтаy2/дельтаx.
Перейдя здесь к пределу при дельтаx0, получим формулу (10.21).
2) Пусть y2 = y1y2; тогда
дельта y = ( y1 + дельтаy1)( y2 + дельтаy2)) - y1y2 = y2y1 + y2дельтаy1 + y1дельтаy2 + дельтаy1дельтаy2,
откуда
дельтаy1/дельтаx = y2дельтаy1/дельтаx + y1дельтаy2/дельтаx. (10.24)
Заметив, что в силу непрерывности функции f2 в точке x0 выполняется условие дельтаy2 = 0, и, перейдя в равенстве (10.24) к пределу при дельтаx0, получим формулу (10.22).
3. Пусть f2(x0)не равно0, и y = y1/y2; тогда
следовательно,
Перейдя здесь к пределу при дельтаx0, получим формулу (10.23). начало
Отметим, что из формулы (10.21) при y2 = 0 (так же, как и из формулы (10.22), когда функция y2 равна постоянной, а поэтому y'2 = 0) следует, что постоянную можно выносить из-под знака дифференцирования, т. е.
(lamday)' = lamday', lamda принадлежит R.
Пример. Вычислим производную функции tg x. Применяя формулу (10.23), получим
Итак,
(tg x)' = 1/cos2x.
Аналогично вычисляется
(ctg x)' = -1/sin2x.
Замечание. Поскольку dx = y'dx, то, умножая формулы (10.21)-(10.23) на dx, получим
d(lamda1 y1 +lamda2 y2) = lamda1dy1 +lamda2 dy',
d(y1y2) = y2dy1 + y1dy2,
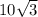, а угол при основании 30, и зная, что катет напротив угла в 30 градусов = половине гипотенузы, то этот катет, она же высота =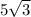 
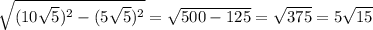
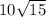
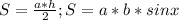
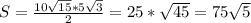
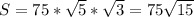
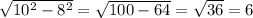
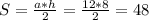
12+2=14км/ч могла быть скорость второго велосипедиста