В классе всего 12 + 18 = 30.
1) Вероятность выбрать первого мальчика равна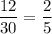 
. Одного человека мы выбрали уже, тогда в классе остается 11 мальчиков и 18 девочек. Вероятность выбрать второго мальчика равна 
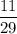. По теореме умножения, искомая вероятность: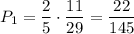 
2) Выбрать первую девочку можно с вероятностью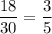 
. В классе остается 29 человек из них 17 девочек. Вероятность выбрать вторую девочку равна 
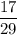. По теореме умножения, искомая вероятность: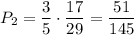 
3) Вероятность того, что среди двух выбранных человек окажутся девочка и мальчик, равна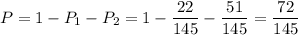 
ответ: 1) 22/145; 2) 51/145; 3) 72/145.
2)32*13500=432000(к.)
1)32*54=1728(к.)-1 коробка
2)1728*250=432000(к.)