тургенев иван сергеевич
(28.10.1818- 22.08.1883)
прозаик, поэт, драматург, критик, публицист, мемуарист, переводчик. родился в семье сергея николаевича и варвары петровны тургеневых. отец, отставной кавалерийский офицер, происходил из старинного дворянского рода, мать – из малородовитой, но богатой помещичьей семьи лутовиновых. детство тургенева прошло в родительском имении спасском-лутовинове, близ г. мценска орловской губернии; первым его учителем был крепостной секретарь его матери федор лобанов. в 1827 г. тургенев переехал с семьей в москву, где продолжил свое образование в частных пансионах, затем под руководством московских педагогов погорельского, дубенского и клюшникова, позднее известного поэта. к 14 тургенев свободно говорил на трех иностранных языках и успел познакомиться с лучшими произведениями европейской и . в 1833 г. он поступил в московский университет, а в 1834 г. перевелся в петербургский, где окончил в 1837 г. словесное отделение философского факультета.
в студенческие годы тургенев начал писать. его первыми поэтическими опытами были переводы, небольшие поэмы, лирические стихотворения и драма «стено» (1834), написанные в модном тогда романтическом духе. среди университетских профессоров тургенева выделялся плетнев, один из близких друзей пушкина, «наставник старого века… не ученый, но по-своему – мудрый». познакомившись с первыми произведениями тургенева, плетнев объяснил юному студенту их незрелость, но выделил и напечатал 2 наиболее удачных стихотворения, побуждая ученика продолжить занятия .
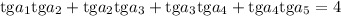
Выразим через третий член и разность прогрессии все остальные члены:
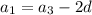
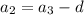
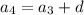
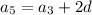
Подставим получившиеся соотношения в уравнение:
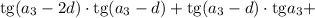
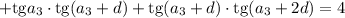
Применяем формулы тангенса суммы и тангенса разности:
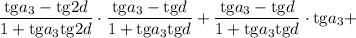
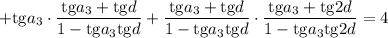
Из имеющегося соотношения для разности прогрессии выразим величины 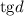 и
и 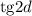 :
:
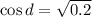
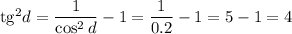
1) 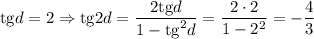
2) 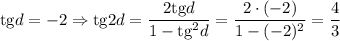
Первый случай: 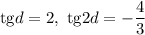
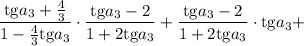
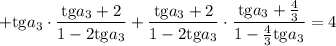
Замена: 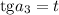
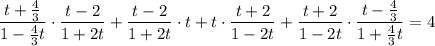
Числитель и знаменатель первой и последней дроби умножим на 3:
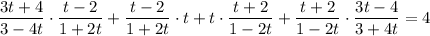
Складываем первые два слагаемых левой части уравнения:
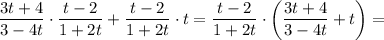
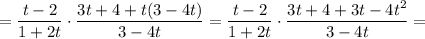
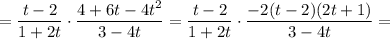
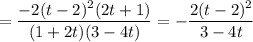
Складываем последние два слагаемых левой части уравнения:
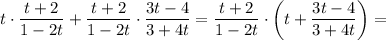
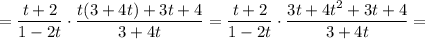
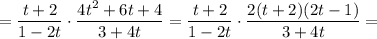
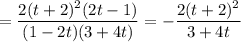
Складываем две получившиеся в предыдущих пунктах величины:
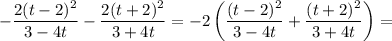
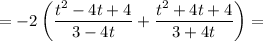
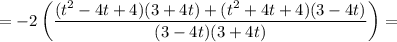
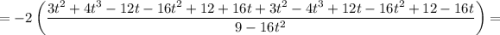
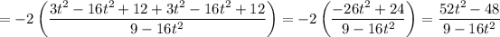
Тогда, уравнение примет вид:
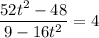
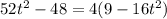
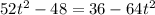
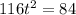
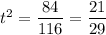
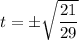
Обратная замена: 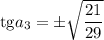
Находим требуемую величину:
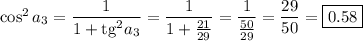
Второй случай: 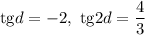
Заметим, что при подстановке этих значений в уравнение, получится такое же уравнение, как и в предыдущем случае с той лишь разницей, что первое и четвертое, а также второе и третье слагаемое будут поменяны местами. Значит, никаких новых результатов получено не будет.
ответ: 0.58