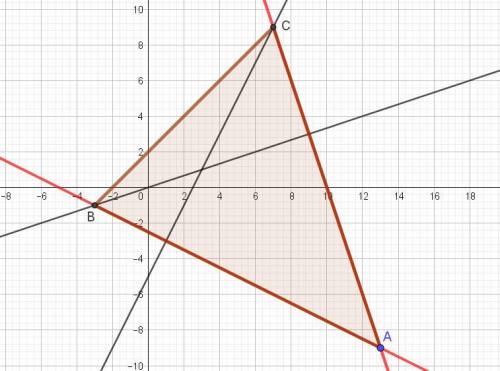
Чтобы узнать, какой вершине треугольника принадлежат координаты точки (13; -9), надо эти координаты подставить в уравнения заданных высот, проведенных из вершин В и С.
При проверке - не подходят, значит, это вершина А.
В уравнениях сторон АВ и АС угловые коэффициенты отрицательно обратны высотам.
АС: у = -3х + в. Подставим координаты точки А:
-9 = -3*13 + в, отсюда в = 39 - 9 = 30.
Получили уравнение стороны АС: у = -3х + 30.
Теперь можно найти координаты точки С, приравняв уравнения АС и высоты к АС: -3х + 30 = 2х - 5, 5х = 35, х = 35/5 = 7, у = -3*7 + 30 = 9.
Точка С(7; 9).
Аналогично определяем координаты точки В( -3; -1).
А) 5/18
В) 2/9
С) 1/9
Пошаговое объяснение:
P=m/n - классическое определение вероятности, где n - число всех равновозможных элементарных исходов, m - число благоприятствующих событию исходов.
n=6*6=36 - всего исходов
Событие А - "сумма числа очков не превосходит 5"
(1;1), (1;2), (1;3), (1;4), (2;1), (2;2), (2;3), (3;1), (3;2), (4;1) - 10 исходов
Р(А)=10/36 = 5/18
Событие В - "произведение числа очков не превосходит 4"
(1;1), (1;2), (1;3), (1;4), (2;1), (2;2), (3;1), (4;1) - 8 исходов
Р(В)= 8/36 = 2/9
Событие С - "произведение числа очков делится на 8"
(2;4), (4;4), (4;6), (6;4) - 4 исхода
Р(С)= 4/36 = 1/9
События совместны, поэтому вероятности перемножатся.
Вероятность того, что первое взятое изделие будет некачественным, равна 3/10.
Вероятность, что второе изделие будет некачественным, равна 2/9.
Итого 1/15.