∠ABD = 21°.
Пошаговое объяснение:
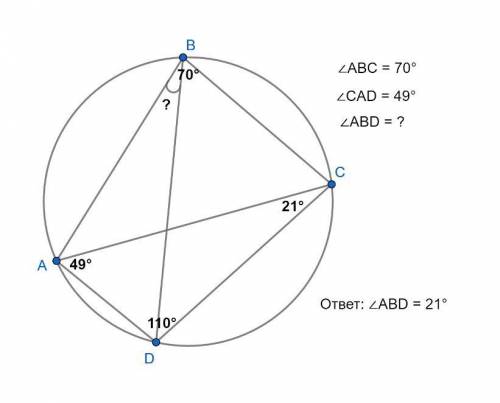
Рисунок прилагается.
Если четырехугольник вписан в окружность, то сумма его противолежащих углов равна 180°.
∠ABC + ∠ADC = 180° ; ∠ABC = 70° по условию.
∠ADC = 180° - ∠ABC = 180° - 70° = 110°;
Сумма углов треугольника = 180°. В ΔCAD ∠CAD = 49° по условию, ∠ADC = 110°; ∠ACD = 180° - ∠CAD - ∠ADC = 180° - 49° - 110° = 21°.
Вписанные углы, опирающиеся на одну и ту же хорду окружности, равны между собой.
∠ABD и ∠ACD вписанные углы, опирающиеся на одну хорду AD.
∠ABD = ∠ACD = 21°.
1) 6 7/12 - 3 17/36=6 21/36 - 3 17/36=3 4/36=3 1/9
2) 3 1/9 * 2,5=28/9 * 5/2=70/9=7 7/9
3) 4 1/3 : 0,65=13/3 * 20/13=20/3=6 2/3
4) 7 7/9 - 6 2/3=7 7/9 - 6 6/9=1 1/9