Возрастает на (-∞;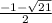
), дальше убывает на (
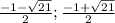) и снова возрастает на (
;+∞).
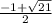Пошаговое объяснение:
Найдём производную исходной функции, пользуясь правилами дифференцирования:
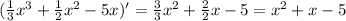
Чтобы найти промежутки монотонности, найдём точки смены монотонности. Они достигаются при равенстве производной нулю. Решим соответствующее уравнение:
⇔ 
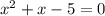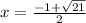или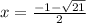 
.
Так мы получили точки смены монотонности. Очевидно, что функция возрастает на промежутке (-∞;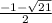) - это легко показать на конкретных значениях, а значит можно восстановить все остальные промежутки так, как показано в ответе.
6(ост1) или 6,1(6)
Пошаговое объяснение:
если укладывать в ряд по 10 плиток, то для квадратной площадки плиток не хватает"
Значит плиток меньше, чем 100 штук.1(
При укладывании по 8 плиток в неполном ряду может быть только 7 плиток, т.к. при укладывании по 9 плиток получается неполный ряд, в котором на 6 плиток меньше. То есть 1 плитка.
Нужно найти такое число меньше 100, которое при делении на 8 даёт остаток 7, а при делении на 9 - остаток 1. Это число 55.
55:8 = 6 (ост. 7)
55:9 = 6 (ост. 1)
или 6,1(6)
2)8*2=16ч
3)-
4)-
5)6*36=216ч
6)12*14=168ч
7)-
8)-